Introduction

This package has been created to automatically identify inlet and outlet of meshes. Such inlet/outlet are geometrically distinguished from other boundary surfaces. Specifically, they are encircled by a closed curve that has sharper normal change and inside area of the curve has more flattened surface. We call these boundaries Feature Surfaces. An example is both ends of a cylinder. Each end is a flat surface that is engulfed with a circle. The two end circles on a cylinder mesh have sharper normal vector change across their points. Figure 1 shows detection of two featured surfaces on a mesh model.

The Feature Surface can be used either as a a plugin for ParaView, a filter in a VTK code or as a standalone application. The program accepts various cell types. Multiple file formats are supported as well. Common file formats are legacy *.vtk and binary *.vtu extensions.

An example of two separated featured surface detection on AAA mesh.

Build Source

User can build the code from source. You can obtain the source code from github repository. Please install git package:

$ sudo apt-get install git

Then, create a build directory and download the source code inside the build directory:

$ mkdir /tmp/FeatureSurface
$ cd /tmp/FeatureSurface
$ git clone git://github.com/ameli/feature-surface

Now, build the code:

$ cmake .
$ make
$ sudo make install
$ cd ..
$ rm -r /tmp/feature-surface

Installation is system-wide for all users.

Program Usage

You can use the program either in terminal or as a ParaView plugin. Here are examples to use it in terminal:

$ featuresurface /input-path/inputfile.vtk outputfile.vtk

For help, use -h, for get program information use -i and for see the license, use -l options.

$ featuresurface -h
$ featuresurface -i
$ featuresurface -l

ParaView Plugin Usage

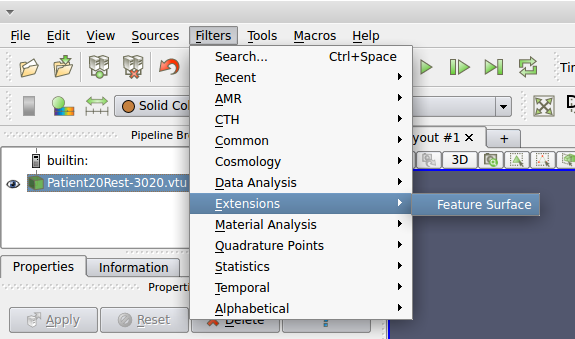
After loading the plugin in ParaView, you can use the filter in Filter menu under Extensions. Figures 2 shows how to apply the plugin inside ParaView.

Using the plugin in ParaView

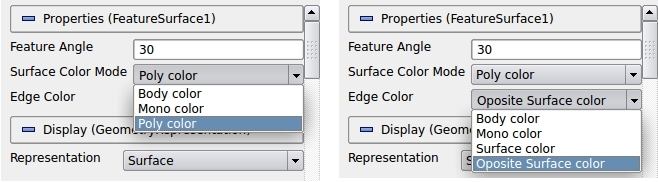
Figure 3 illustrated the options that can be set in ParaView for this filter. Filter has the following options:

Feature angle is the threshold angle degree for which the edges are detected. Smaller feature angle is less restrictive.
Surface color can be one of the followings:
- Body color: Assigns the color 0 to all featured surface points. This is the same color as body.
- Mono color: Assigns color 1 for all features surface points.
- Poly color: For each group of points in a features surface area, it assigns an integer, starting from 1. Thus the n-th features surface has the color n.
Edge color can be one of the followings:
- Body color: Assigns the color 0 to all edge points. This is the same color as body.
- Mono color: Assigns color 1 for all edge points.
- Surface color: Assigns the color of the surface that the edge is belonging to.
- Opposite Surface color: Assigns opposite of the color of surface that edge is belonging to. For instants, if the surface has color n, then its edge has color -n.

Left: Options for surface color mode. Right: Options for Edge color mode.

Robustness of Algorithm

The algorithm that is used for this filter is robust in variety of ways. Such robustness was gained by both geometrical and topological checks on edge extraction. The following are a brief description.

Geometrical Checks

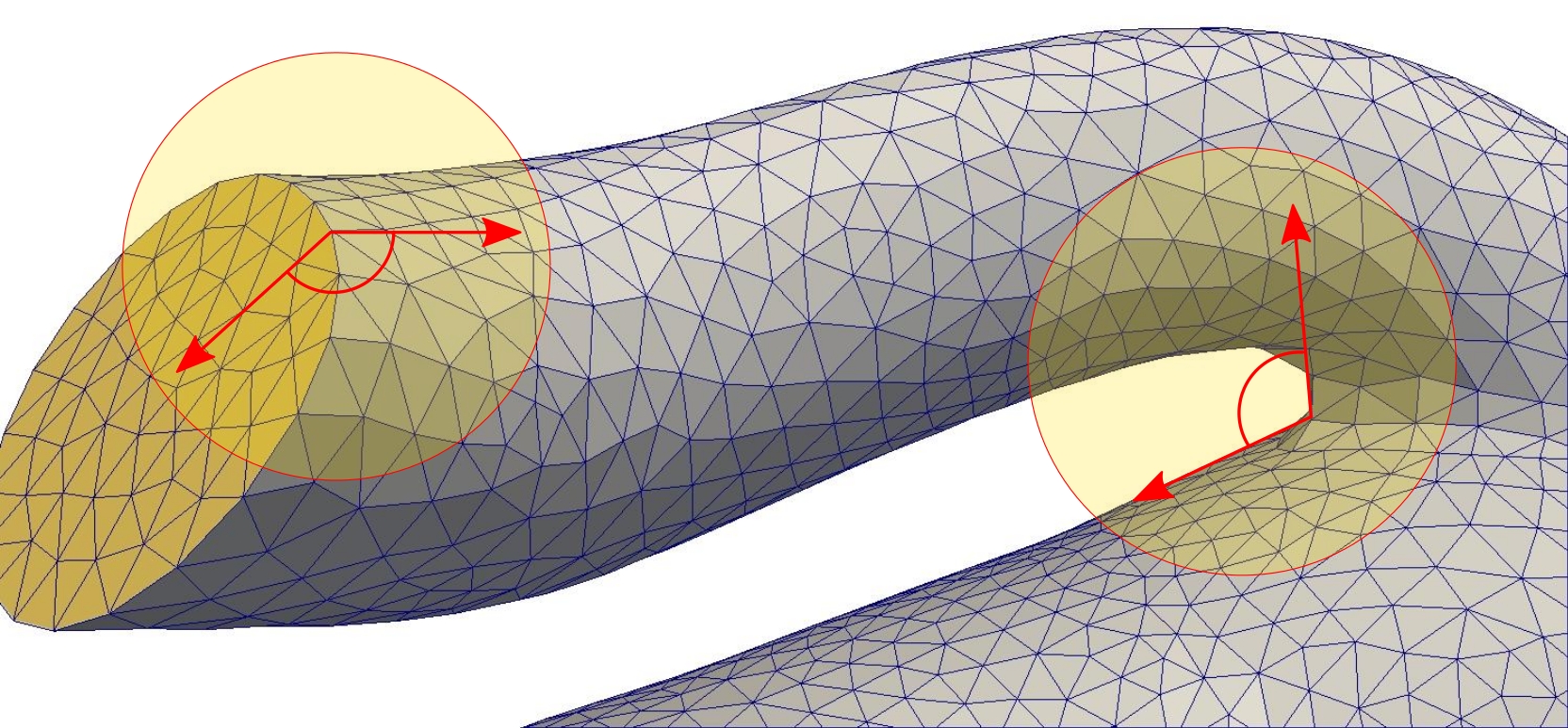
First, the algorithm is not sensitive on Edge Angle. Majority of function were used to eliminate this dependency, so a broad range of edge angle can lead to reasonable edge detection. Figure 4 shows two violations of edge angles in critical situations. In the left highlighted spot, edge angle is small, and an rudimentary search might not detect the edge and featured surface at all. User might lower the edge angle threshold in settings, but it comes with the cost of detecting some edges that are not belong to an interesting featured surface. For instance, the right highlighted spot has a large edge angle but it is not considered as inlet or outlet. However a simple algorithm might detect the edge and try to extract a spurious feature surface. By using a geometrical checks we eliminate such spurious edges.

Left and right spotlights are two angles that violates with edge angle threshold.

Topological Checks

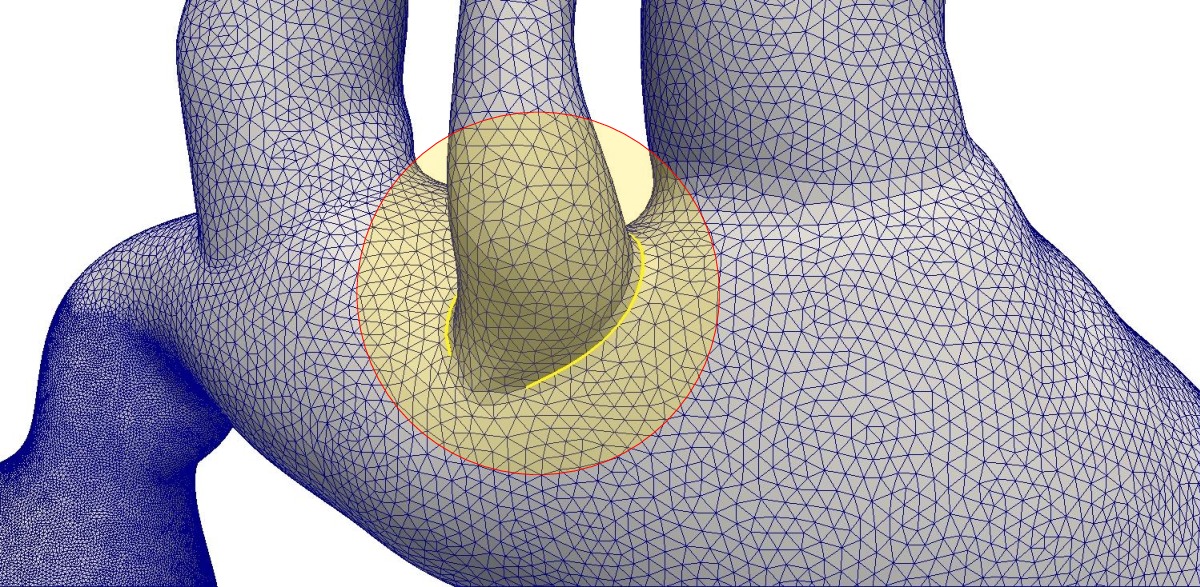
A more basic issue with edge extraction is the topology of edge itself. Some edges are not closed curve, some are having more than two connectivities at each points, or multiple closed curves are sharing a set of common points. Few of these unusual edges are not accepted as an edge for a featured surface, and some needs trimming of excessive points. Since excessive points are not known priori, all possible routes on the edges should be checked for finding a nice curve that can be a candidate for a featured surface. Figure 5 illustrate such spurious edges that should take out of results. This listing is the program output applied on data in figure 5.

An example of spurious edge that does not construct a featured surface.

Output of program $ ./FeatureSurface

Closed polygon found. Number of points: 21
Closed polygon found. Number of points: 48
Closed polygon found. Number of points: 60
Closed polygon found. Number of points: 118
Closed polygon found. Number of points: 37
Closed polygon found. Number of points: 18

Fatal Point: 19, Number of connectivities: 3
Fatal Point: 19, Number of connectivities: 3
Fatal Point: 33, Number of connectivities: 3
Fatal Point: 32, Number of connectivities: 1
Fatal Point: 39, Number of connectivities: 1
Fatal Point: 64, Number of connectivities: 1
Total number of closed polygons: 6

Closed Edge: 1,  Surface points found: 39
Closed Edge: 2,  Surface points found: 206
Closed Edge: 3,  Surface points found: 315
Closed Edge: 4,  Surface points found: 1270
Closed Edge: 5,  Surface points found: 120
Closed Edge: 6,  Surface points found: 23

Orientating Edges

An important issue after extracting a candidate edge curve is to find an appropriate orientation on edge; that is, finding which side is interior or exterior of the closed curve. Topologically, both sides ca be interior since a smooth homotopy can make both side identical. Rather using topologically distinct sides, we use geometrically distinct regions. We define an interior side where the surface is tend to be more flattened. This assumption is natural in inlet and outlets of computational meshes. The algorithm that is used in the filter can decide which surface to be interior.

However, in rare cases, due to incorrect meshing or unusual cases the interior and exterior surfaces of an edge can be related with a path other than the edge itself. The current code can identify such cases and avoid colorizing the while domain. This feature makes the algorithm very robust in colorizing domains correctly.

Examples

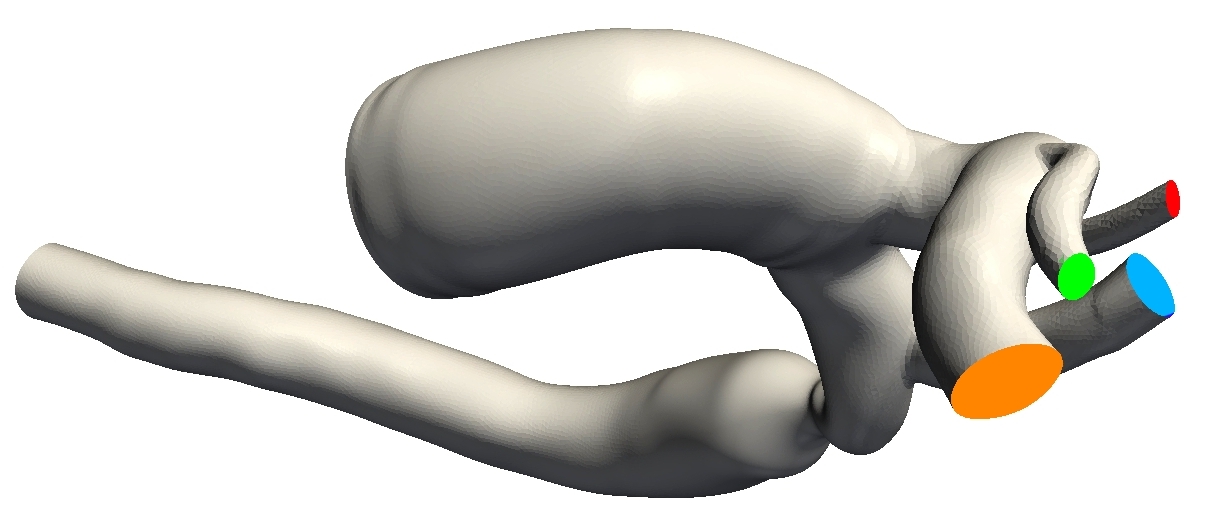
The filter's performance has been tested on two mesh models on both Linux and Mac OS X operating systems using both command line and ParaView plugin. Figure 6 shows the application of filter on AAA mesh model. The mesh has 11 inlet and outlets that all of them has been detected by the filter. With no surprise, the performance was not sensitive to selecting the Edge angle, thus all features identified without including any noisy edge or non-interesting edges. Figure 7 illustrates the application of the filter on Aortic mesh model, which all 6 inlet or outlets were detected. Since the algorithm re-uses all of its computed data during process at each iterative search on edges, the algorithm is fast. It takes only 4 or 5 seconds for a million element Aortic mesh to finish the computation.

AAA mesh with 11 featured surface detected.

As described in this section, the plugin has options to colorize the edges and/or surfaces in multiple ways. Edges and their corresponding surfaces can be colorized with the same color, body color or independently.

Aortic mesh with 6 featured surface detected.

License

This source code is provided as-is, without any express or implied warranty. In no event will the author be held liable for any damages arising from the use of this software.

Permission is granted to anyone to use this software for non commercial purpose, to alter it and redistribute it freely, subject to the following restrictions:

The origin of this source code must not be misrepresented; you must not claim that you wrote the original source code.
You may modify or alter the source code at your own risk, provided that such modifications are extensively commented. Altered source versions must not be misrepresented as being the original source code.
Source code may not be redistributed in any way. You may distribute the target binary for non-commercial purposes.
If you use this source code in a non-commercial product, an acknowledgment in the product documentation would be appreciated.
This notice may not be removed or altered from any source distribution.

Bug Report

Any bug reports and comments are appreciated. You may report bugs in github, Launchpad or send email.

Acknowledgement

This work was supported by the National Science Foundation, award number 1047963.