Quick Start#

This is a quick tutorial to demonstrate basic usage of G-Learn package.

Import#

Import the package using:

[1]:

import glearn

Prior to starting, you can verify the G-Learn version, the number of available CPU processors, connected GPU devices, and the memory usage of the current Python process using:

[2]:

glearn.info()


glearn version  : 0.21.1
imate version   : 0.18.0
processor       : Intel(R) Core(TM) i5-2520M CPU @ 2.50GHz
num threads     : 4
gpu device      : not found
num gpu devices : 0
cuda version    : not found
nvidia driver   : not found
process memory  : 124.6 (Mb)

Generate Points#

We generate a set of 50 points randomly distributed in the interval \(\mathcal{D} = [0, 1]\), where \(90\%\) of the points are concentrated in the sub-interval \([a=0.4, b=0.6]\) with a uniform distribution, while the remaining points are uniformly spread elsewhere.

To create such a set of points for simplicity, you can use the glearn.sample_data module.

[3]:

from glearn import sample_data
x = sample_data.generate_points(num_points=50, dimension=1,
                                grid=False,a=0.4, b=0.6,
                                contrast=0.9, seed=42)

Generate Noisy Data#

On the set of points \(\boldsymbol{x} = (x_1, \dots, x_d) \in \mathcal{D} \in \mathbb{R}^d\) (where \(d=1\) as specified above), we define a stochastic function:

\[y(\boldsymbol{x}) = \sum_{i=1}^d \sin\left(\pi x_i \right) + \epsilon,\]

where \(\epsilon\) is a random variable \(\epsilon(x) \sim \mathcal{N}(0, \sigma_0^2)\) with a noise standard deviation of \(\sigma_0 = 0.05\).

You can generate the random data described above using the glearn.sample_data module.

[4]:

y_noisy = sample_data.generate_data(x, noise_magnitude=0.1, plot=True)
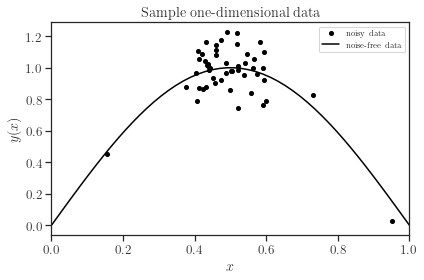
../_images/tutorials_quick_start_7_0.png

The figure above illustrates the noisy data (represented as dots) alongside the original noise-free function (depicted as a solid curve). It’s worth noting that the majority of data points are concentrated within the sub-interval \([0.4, 0.6]\), while outside this interval, data points are sparsely distributed.

Later on, we will demonstrate accurate predictions within the concentrated sub-interval and less precise predictions outside of it.

Stochastic Model for Noisy Data#

We model the random data \(z\) by

\[y(x) = \mu(x) + \delta(x) + \epsilon(x),\]

where

  • \(\mu(x)\) is a deterministic mean function.

  • \(\delta(x)\) is a zero-mean stochastic function and will be determined later.

  • \(\epsilon(x)\) is a zero-mean stochastic function representing the input noise and characterized by the discrete covariance:

\[\mathbb{E}[\epsilon(x), \epsilon(x')] = \sigma_0^2 \mathbf{I}\]

where \(\mathbf{I}\) is the identity matrix, and the hyperparameter \(\sigma_0^2\) is the variance of the noise. We assume the noise variance is not known.

Design Matrix#

We represent the deterministic mean function \(\mu\) by the linear model \(\mu(\boldsymbol{x}) = \boldsymbol{\phi}(x)^{\intercal} \boldsymbol{\beta}\) as a linear combination of basis functions:

\[\boldsymbol{\phi}(x): \mathcal{D} \to \mathbb{R}^m,\]

and \(\beta \in \mathbb{R}^{m}\) are the parameters. On discrete points \(\boldsymbol{x}\), the set of basis functions are disretized to the design matrix \(\mathbf{X} \in \mathbf{R}^{n \times m}\)

\[X_{ij} = \phi_{j}(\boldsymbol{x}_i)\]

Other ways to contrust the design matrix are by trogonometric functions, hyperbolic functions, user-defined custom functions, or a combination of all. Here we only use a fifth order monomial as follows:

\[\boldsymbol{\phi}(\boldsymbol{x}) = (1, x, \cdots, x^4)^{\intercal}.\]

Hence, \(m = 5\).

Prior for Parameter \(\boldsymbol{\beta}\)#

We also prescribe a normal prior to the unknown parameter \(\boldsymbol{\beta}\):

\[p(\boldsymbol{\beta} | \sigma^2) \sim \mathcal{N}(\boldsymbol{b}, \sigma^2 \mathbf{B}),\]

where \(\sigma^2 \mathbf{B} \in \mathbb{R}^{m \times m}\) is the covariance of \(\boldsymbol{\beta}\). The hyperparameter \(\sigma^2\) is the variance of the regression and is not known.

[5]:

# Mean of hyperparameter beta.
# The size of b should be m, the number of columns of design matrix X.
import numpy
b = numpy.zeros((6, ))

# Generate a random matrix B for covariance of beta.
# The shape of matrix B should be (m, m)
numpy.random.seed(0)
B = numpy.random.rand(b.size, b.size)

# Making sure the covariance matrix B positive-semidefinite
B = 1e+5 * B.T @ B

Linear Model#

The linear model of mean \(\mu = \mathbf{X} \boldsymbol{\beta}\) can be created by glearn.mean.LinearModel class:

[6]:

# Create mean object using glearn.
mean = glearn.LinearModel(x, polynomial_degree=5, b=b, B=B)

Kernels#

The zero-mean stochastic function \(\delta(x): \mathcal{D} \to \mathbb{R}\) is characterized by its covariance:

\[\mathbb{E}[\delta(x), \delta(x')] = k(x, x'|\boldsymbol{\alpha}).\]

The function \(k: \mathcal{D} \times \mathcal{D} \times \mathbb{R}^d \to \mathbb{R}\) is the correlation kernel and can be created using the glearn.kernel module. Various kernels available in this module, including:

  • Matern()

  • Exponential()

  • SquareExponential()

  • RationalQuadratic()

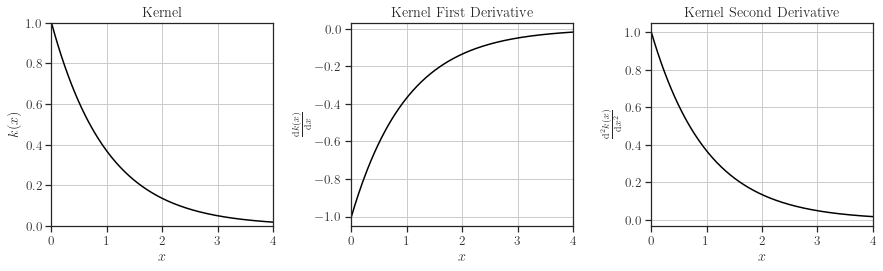
In this example, we will use the exponential kernel.

[7]:

from glearn import kernels
kernel = kernels.Exponential()
kernel.plot()
../_images/tutorials_quick_start_15_0.png

Scale Hyperparameter#

The hyperparameters \(\boldsymbol{\alpha} = (\alpha_1, \dots, \alpha_d) \in \mathbb{R}^d\) determine the scale of each spatial dimension. In our example, \(d=1\). The scale can be either explicitly given if known or characterized by a prior distribution \(p(\boldsymbol{\alpha})\) using the glearn.priors class. A list of available priors includes:

  • Uniform

  • Cauchy

  • StudentT

  • InverseGamma

  • Normal

  • Erlang

  • BetaPrime

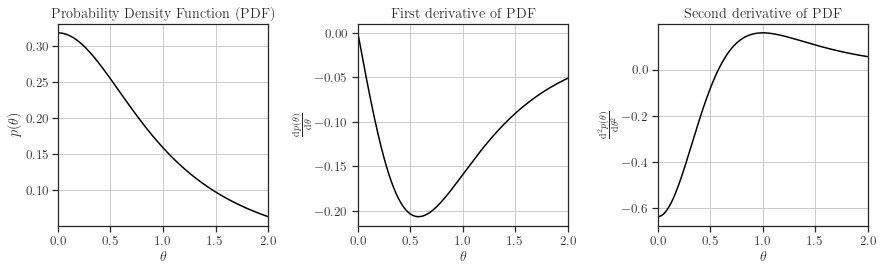
In this context, we are using the Cauchy prior. We will also plot the prior and its first and second derivatives.

[8]:

from glearn import priors
scale = priors.Cauchy()
scale.plot()
../_images/tutorials_quick_start_17_0.png

Covariance#

The covariance of the model is given by

\[\boldsymbol{\Sigma}(\sigma^2, \sigma_0^2, \boldsymbol{\alpha}) = \sigma^2 \mathbf{K}(\boldsymbol{\alpha}) + \sigma_0^2 \mathbf{I},\]

where

\[\mathbf{K}(\boldsymbol{\alpha}): \mathbb{R}^{d} \to \mathbb{R}^{n \times n},\]

and \(\mathbf{I}\) is the identity matrix.

An object of the above covariance model can be created using the glearn.Covariance class.

[9]:

cov = glearn.Covariance(x, kernel=kernel, scale=scale)

Gaussian Process#

The Gaussian process is defined as

\[z \sim \mathcal{GP}(\mu, \boldsymbol{\Sigma})\]

and can be created using the glearn.GaussianProcess class with the mean and covariance objects.

[10]:

gp = glearn.GaussianProcess(mean, cov)

Training Hyperparameters#

The hyperparameters \((\sigma, \sigma_0, \boldsymbol{\alpha})\) and the parameter \(\boldsymbol{\beta}\) can be trained via the gp.train() function.

The type of profiling for the likelihood function can be set by the profile_hyperparam argument, which can take one of the following values:

  • 'none': no profiling

  • 'var': profiling on variance hyperparameter.

  • 'var_noise': profiling on both variance and noise hypeprarameter.

The optimization method can be set by optimization_method and can be one of:

  • 'chandrupatla': requires jacobian

  • 'brentq': requires jacobian

  • 'Nelder-Mead': requires func

  • 'BFGS': requires func, jacobian

  • 'CG': requires func, jacobian

  • 'Newton-CG': requires func, jacobian, hessian

  • 'dogleg': requires func, jacobian, hessian

  • 'trust-exact': requires func, jacobian, hessian

  • 'trust-ncg': requires func, jacobian, hessian

The internal matrix algebra of this object can be set via the imate_method argument, which can take a value from one of the followings:

  • 'eigenvalue': using eigenvalue method.

  • 'cholesky': using Cholesky method.

  • 'hutchinson': using stochastic Hutchinson method.

  • 'slq': using stochastic Lanczos quadrature method.

Here we use the Cholesky method.

[11]:

profile_hyperparam = 'var'
optimization_method = 'Newton-CG'
imate_options = {'method': 'cholesky'}
hyperparam_guess = None
result = gp.train(y_noisy, profile_hyperparam=profile_hyperparam,
                  log_hyperparam=True, hyperparam_guess=hyperparam_guess,
                  optimization_method=optimization_method, tol=1e-6,
                  max_iter=1000, use_rel_error=True, imate_options=imate_options,
                  verbose=True, plot=False)


          Error
=========================
itr   param  1   param  2
---   --------   --------
001        inf        inf
002   8.87e-02   5.89e-03
003   6.06e-03   2.44e-01
004   3.09e-03   8.21e-02
005   1.35e-04   9.87e-03
006   2.10e-06   1.45e-04
007   0.00e+00   0.00e+00

                                Training Summary
================================================================================
       posterior/param                optimization              imate solver
-----------------------------      -------------------      --------------------
posterior    +2.355328920e+01      method    Newton-CG      method      cholesky
eta          7.9209829878e+01      tol        1.00e-06      tol         1.00e-08
sigma        1.3028753864e-02      max iter       1000      interpolate    False
sigma0       1.1595578487e-01      max bracket try   6      min num samples    0
alpha        1.2929866862e-01      profile param   var      max num samples    0

                                    Process
================================================================================
         time (sec)                    evaluations               processor
-----------------------------      -------------------      --------------------
task         clock    process      task              #      device             #
================================================================================
correlation  2.81e-1  1.03e+0      correlation      23      cpu threads        4
logdet       2.79e-3  9.24e-3      likelihood        8      gpu devices        0
traceinv     8.48e-3  2.98e-2      jacobian          8      gpu multiproc      0
solver       1.15e-1  4.33e-1      hessian           7      gpu thrds/sm       0
overall      5.45e-1  1.85e+0      optimization      7      mem used (b) 1585152

Prediction#

After training the hyperparameters, the gp object is ready to predict the data on new points. First, we create a set of \(1000\) test points \(x^{\star}\) equally spaced in the interval \([0, 1]\).

[12]:

# Generate test points
test_points = sample_data.generate_points(num_points=1000, dimension=1, grid=True)

For the sake of comparison, we also generate the noise-free data on the test points, \(z(x^{\star})\), using zero noise with \(\sigma_0 = 0\).

[13]:

# True data (without noise)
z_true = sample_data.generate_data(test_points, noise_magnitude=0.0)

Note that the above step is unnecessary and only used for the purpose of comparison with the prediction since we already know the exact function that generated the noisy data \(z\) in the first place.

The posterior predictive distribution of the prediction \(z^{\star}(x^{\star})\) is of the form

\[z^{\star}(x^{\star}) \sim \mathcal{N}\left(\mu^{\star}(x^{\star}), \mathbf{\Sigma}^{\star \star}(x^{\star}, x'^{\star})\right)\]

where:

  • \(\mu^{\star}\) is the posterior predictive mean, and

  • \(\mathbf{\Sigma}^{\star \star}\) is the posterior predictive covariance between test points and themselves.

Prediction can be made using the gp.predict() function.

[14]:

z_star_mean, z_star_cov = gp.predict(test_points, cov=True, plot=True,
                                     confidence_level=0.95,
                                     true_data=z_true, verbose=True)


                               Prediction Summary
================================================================================
               process                                    config
-------------------------------------      -------------------------------------
wall time (sec)               1.95e-1      num training points                50
proc time (sec)               6.88e-1      num test points                  1000
memory used (b)              21159936      compute covariance               True
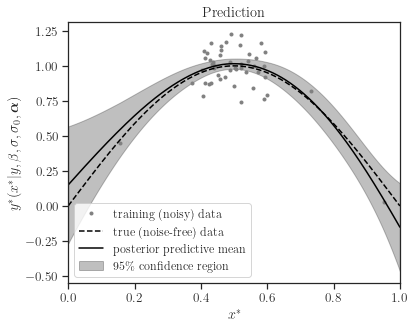
../_images/tutorials_quick_start_29_1.png

By setting the boolean argument cov=False, the predictive covariance is not computed, which enhances computational speed.

  • When cov=True, meaning that both \(\mu^{\star}\) and \(\mathbf{\Sigma}^{\star \star}\) are computed, the prediction process is \(\mathcal{O}\left((n^{\star})^3\right)\) complex.

  • In contrast, when cov=False to only compute \(\mu^{\star}\), the prediction process is only \(\mathcal{O}\left((n^{\star})^2\right)\) complex.

Furthermore, when cov=False, once the first prediction on a set of test points \(\left\{ x_i^{\star} \right\}_{n^{\star}}\) is made, the future calls to the predict() function are of order \(\mathcal{O}(n^{\star})\), even when applied to a different set of test points. This is because the gp object stores all internal computations that are independent of the test points.

[15]:

z_star_mean = gp.predict(test_points, cov=False, verbose=True)


                               Prediction Summary
================================================================================
               process                                    config
-------------------------------------      -------------------------------------
wall time (sec)               2.18e-2      num training points                50
proc time (sec)               5.16e-2      num test points                  1000
memory used (b)                     0      compute covariance              False