get_instructions_per_flop#
- detkit.get_instructions_per_flop(task='matmul', dtype='float64', impl='native', min_n=100, max_n=500, num_n=6, plot=False)#
Counts the hardware instructions of computing a single FLOP of a benchmark task on the current processor.
The goal of this function is to be used to measure the computational complexity of an algorithm. To measure the complexity, we use floating point operations (FLOPs). We define a FLOP by a fused multiply-add operation.
FLOPs cannot be directly measured on the processor. Instead, we measure the hardware instructions of the processor. To measure the FLOPs of an algorithm, we can divide the instructions it takes to run the desired algorithm by the instructions it takes to compute a single FLOP of another benchmark task the same processor and same compiler configuration. The aim of this function is to measure the instructions of a unit FLOP.
A benchmark task is a basic mathematical operation, such as matrix-matrix multiplication, LU factorization, or Cholesky decomposition on a matrix. Assuming the matrix size is \(n\), the complexity of either of the tasks provided in are as follows
Code name
Task name
Complexity
'matmul'matrix-matrix multiplication
\(n^3\)
'gramian'Gramian matrix multiplication
\(\frac{1}{2}n^3\)
'cholesky'Cholesky decomposition
\(\frac{1}{3}n^3\)
'plu'PLU decomposition
\(\frac{2}{3}n^3\)
'lu'LU decomposition
\(\frac{2}{3}n^3\)
This function measures the instructions of a benchmark task as \(n\) tends to infinity.
- Parameters:
- task{‘matmul’, ‘gramian’, ‘cholesky’, ‘lu’, ‘plu’}, default=’matmul’
The benchmark task to count its hardware instructions.
'matmul': matrix-matrix multiplication task.'gramian': Gramian matrix-matrix multiplication task.'cholesky': Cholesky decomposition task.'lu': LU decomposition task.'plu': PLU decomposition task.
- dtype{‘float32’, ‘float64’, ‘float128’}, default=’float64’
The type of the test data.
- impl{
'detkit','lapack','blas'}, default:'native' Implementation to execute the benchmark.
'native': uses native implementation of tasks (on single thread).'lapack': uses LAPACK implementation of tasks using scipy.'blas': uses BLAS implementation of tasks using numpy.
- min_nint, default=100
Minimum square matrix size to be tested.
- max_nint, default=500
Maximum square matrix size to be tested.
- num_nint, default=10
Number of various matrix sizes to try.
- plotbool, default=False
If True, the estimation of FLOPs versus various matrix sizes is plotted.
- Returns:
- instint
Count of hardware instructions. If the operating system or the processor does not support the feature of counting the hardware instructions, -1 is returned.
See also
Notes
Instructions count depends on the processor and the compiler configurations that compiles the package. Results may vary on different computers.
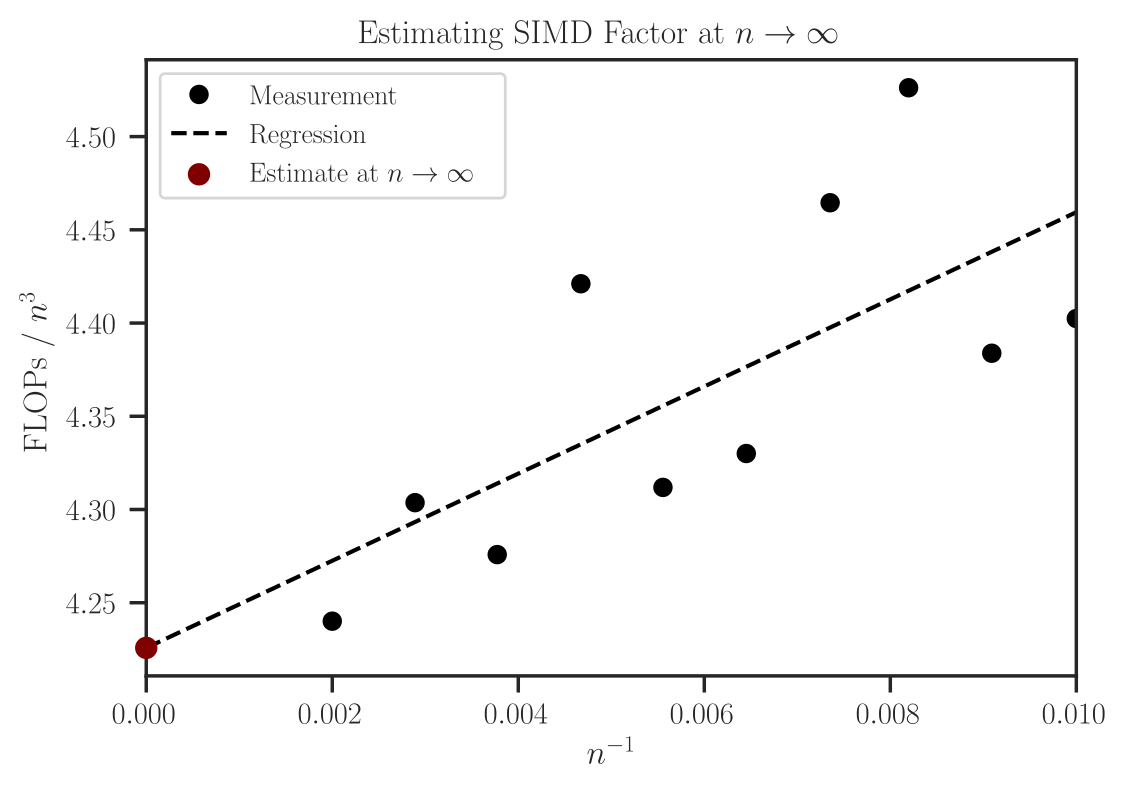
Instruction counts, \(c\), also varies by the size of the matrices used in the benchmark test, but it converges when the matrix size, \(n\) is very large. To obtain a unique number, we use the following asymptotic relation:
\[c(n) = c_{\infty} + \frac{\alpha}{n}\]To measure \(c_{\infty}\), this function measures \(c(n)\) on several matrix sizes \(n\) and uses the above relation to find their asymptote.
It appears that the choice of dtype does not have an effect on the count of hardware instructions.
Examples
We can measure the FLOPs of computing, for instance, loggdet as follows:
>>> import numpy >>> from detkit import loggdet, get_instructions_per_count >>> # Generate a random matrix >>> n, m = 1000, 500 >>> rng = numpy.random.RandomState(0) >>> A = rng.rand(n, n) >>> X = rng.rand(n, m) >>> # Measure the hardware instructions to compute loggdet of matrix >>> loggdet_, sign, inst = loggdet(A, X, flops=True) >>> print(inst) 11009228170 >>> # Measure hardware instructions of a single FLOP >>> benchmark_inst = get_instructions_per_flop(task='matmul') >>> print(benchmark_int) 5.21 >>> # Calculate FLOPs of loggdet function >>> flops = int(float(inst) / float(benchmark_inst)) >>> print(flops) 2110324959 >>> # Calculate coefficient of complexity >>> print(flops / n**3) 2.11
Example of plotting how the instructions are estimated:
>>> import detkit >>> inst = detkit.get_instructions_per_flop(dtype='float32', min_n=100, ... max_n=500, num_n=10, ... plot=True) >>> # inst is the intercept of the regression line in the plot >>> print(inst) 4.225773707890822