A static class for vector operations, similar to level-1 operations of the BLAS library. This class acts as a templated namespace, where all member methods are public and static. More...

#include <c_vector_operations.h>

Static Public Member Functions
static void	copy_vector (const DataType input_vector, const LongIndexType vector_size, DataType output_vector)
	Copies a vector to a new vector. Result is written in-place. More...

static void	copy_scaled_vector (const DataType input_vector, const LongIndexType vector_size, const DataType scale, DataType output_vector)
	Scales a vector and stores to a new vector. More...

static void	subtract_scaled_vector (const DataType input_vector, const LongIndexType vector_size, const DataType scale, DataType output_vector)
	Subtracts the scaled input vector from the output vector. More...

static DataType	inner_product (const DataType vector1, const DataType vector2, const LongIndexType vector_size)
	Computes Euclidean inner product of two vectors. More...

static DataType	euclidean_norm (const DataType *vector, const LongIndexType vector_size)
	Computes the Euclidean norm of a 1D array. More...

static DataType	normalize_vector_in_place (DataType *vector, const LongIndexType vector_size)
	Normalizes a vector based on Euclidean 2-norm. The result is written in-place. More...

static DataType	normalize_vector_and_copy (const DataType vector, const LongIndexType vector_size, DataType output_vector)
	Normalizes a vector based on Euclidean 2-norm. The result is written into another vector. More...

Detailed Description

template<typename DataType>
class cVectorOperations< DataType >

A static class for vector operations, similar to level-1 operations of the BLAS library. This class acts as a templated namespace, where all member methods are public and static.

See also: MatrixOperations

Definition at line 35 of file c_vector_operations.h.

Member Function Documentation

◆ copy_scaled_vector()

template<typename DataType >

void cVectorOperations< DataType >::copy_scaled_vector	(	const DataType *	input_vector,
		const LongIndexType	vector_size,
		const DataType	scale,
		DataType *	output_vector
	)

static

Scales a vector and stores to a new vector.

Parameters

[in]	input_vector	A 1D array
[in]	vector_size	Length of vector array
[in]	scale	Scale coefficient to the input vector. If this is equal to one, the function effectively becomes the same as copy_vector.
[out]	output_vector	Output vector (written in place).

Definition at line 81 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Using OpenBlas
     int incx = 1;
     int incy = 1;
  
     cblas_interface::xcopy(vector_size, input_vector, incx, output_vector,
                            incy);
  
     cblas_interface::xscal(vector_size, scale, output_vector, incy); 
  
     #else
  
     // Not using OpenBlas
     for (LongIndexType i=0; i < vector_size; ++i)
     {
         output_vector[i] = scale * input_vector[i];
     }
  
     #endif
 }

Referenced by c_lanczos_tridiagonalization(), and cVectorOperations< DataType >::normalize_vector_and_copy().

Here is the caller graph for this function:

◆ copy_vector()

template<typename DataType >

void cVectorOperations< DataType >::copy_vector	(	const DataType *	input_vector,
		const LongIndexType	vector_size,
		DataType *	output_vector
	)

static

Copies a vector to a new vector. Result is written in-place.

Parameters

[in]	input_vector	A 1D array
[in]	vector_size	Length of vector array
[out]	output_vector	Output vector (written in place).

Definition at line 39 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Using Openblas
     int incx = 1;
     int incy = 1;
  
     cblas_interface::xcopy(vector_size, input_vector, incx, output_vector,
                            incy);
  
     #else
  
     // Not using OpenBlas
     for (LongIndexType i=0; i < vector_size; ++i)
     {
         output_vector[i] = input_vector[i];
     }
  
     #endif
 }

Referenced by c_lanczos_tridiagonalization().

Here is the caller graph for this function:

◆ euclidean_norm()

template<typename DataType >

DataType cVectorOperations< DataType >::euclidean_norm	(	const DataType *	vector,
		const LongIndexType	vector_size
	)

static

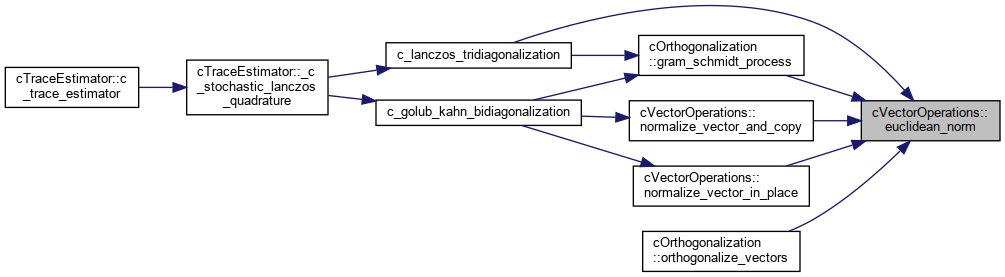
Computes the Euclidean norm of a 1D array.

The reduction variable (here, inner_prod ) is of the type long double. This is becase when DataType is float, the summation loses the precision, especially when the vector size is large. It seems that using long double is slightly faster than using double. The advantage of using a type with larger bits for the reduction variable is only sensible if the compiler is optimized with -O2 or -O3 flags.

Using a larger bit type for the reduction variable is very important for this function. If DataType is float, without such consideration, the result of estimation of trace can be completely wrong, just becase of the wrong norm results. For large array sizes, even libraries such as openblas does not compute the dot product accurately.

The chunk computation of the dot product (as seen in the code with chunk=5) improves the preformance with gaining twice speedup. This result is not much dependet on chunk. For example, chunk=10 also yields a similar result.

Parameters

[in]	vector	A pointer to 1D array
[in]	vector_size	Length of the array

Returns: Euclidean norm

Definition at line 281 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Using OpenBlas
     int incx = 1;
  
     DataType norm = cblas_interface::xnrm2(vector_size, vector, incx);
  
     return norm;
  
     #else
  
     // Compute norm squared
     long double norm2 = 0.0;
     LongIndexType chunk = 5;
     LongIndexType vector_size_chunked = vector_size - (vector_size % chunk);
  
     for (LongIndexType i=0; i < vector_size_chunked; i += chunk)
     {
         norm2 += vector[i] * vector[i] +
                  vector[i+1] * vector[i+1] +
                  vector[i+2] * vector[i+2] +
                  vector[i+3] * vector[i+3] +
                  vector[i+4] * vector[i+4];
     }
  
     for (LongIndexType i=vector_size_chunked; i < vector_size; ++i)
     {
         norm2 += vector[i] * vector[i];
     }
  
     // Norm
     DataType norm = sqrt(static_cast<DataType>(norm2));
  
     return norm;
  
     #endif
 }

Referenced by c_lanczos_tridiagonalization(), cOrthogonalization< DataType >::gram_schmidt_process(), cVectorOperations< DataType >::normalize_vector_and_copy(), cVectorOperations< DataType >::normalize_vector_in_place(), and cOrthogonalization< DataType >::orthogonalize_vectors().

Here is the caller graph for this function:

◆ inner_product()

template<typename DataType >

DataType cVectorOperations< DataType >::inner_product	(	const DataType *	vector1,
		const DataType *	vector2,
		const LongIndexType	vector_size
	)

static

Computes Euclidean inner product of two vectors.

The reduction variable (here, inner_prod ) is of the type long double. This is becase when DataType is float, the summation loses the precision, especially when the vector size is large. It seems that using long double is slightly faster than using double. The advantage of using a type with larger bits for the reduction variable is only sensible if the compiler is optimized with -O2 or -O3 flags.

Using a larger bit type for the reduction variable is very important for this function. If DataType is float, without such consideration, the result of estimation of trace can be completely wrong, just becase of the wrong inner product results. For large array sizes, even libraries such as openblas does not compute the dot product accurately.

The chunk computation of the dot product (as seen in the code with chunk=5) improves the preformance with gaining twice speedup. This result is not much dependet on chunk. For example, chunk=10 also yields a similar result.

Parameters

[in]	vector1	1D array
[in]	vector2	1D array
[in]	vector_size	Length of array

Returns: Inner product of two vectors.

Definition at line 204 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Using OpenBlas
     int incx = 1;
     int incy = 1;
  
     DataType inner_prod = cblas_interface::xdot(vector_size, vector1, incx,
                                                 vector2, incy);
  
     return inner_prod;
  
     #else
  
     // Not using OpenBlas
     long double inner_prod = 0.0;
     LongIndexType chunk = 5;
     LongIndexType vector_size_chunked = vector_size - (vector_size % chunk);
  
     for (LongIndexType i=0; i < vector_size_chunked; i += chunk)
     {
         inner_prod += vector1[i] * vector2[i] +
                       vector1[i+1] * vector2[i+1] +
                       vector1[i+2] * vector2[i+2] +
                       vector1[i+3] * vector2[i+3] +
                       vector1[i+4] * vector2[i+4];
     }
  
     for (LongIndexType i=vector_size_chunked; i < vector_size; ++i)
     {
         inner_prod += vector1[i] * vector2[i];
     }
  
     return static_cast<DataType>(inner_prod);
  
     #endif
 }

Referenced by c_lanczos_tridiagonalization(), cOrthogonalization< DataType >::gram_schmidt_process(), and cOrthogonalization< DataType >::orthogonalize_vectors().

Here is the caller graph for this function:

◆ normalize_vector_and_copy()

template<typename DataType >

DataType cVectorOperations< DataType >::normalize_vector_and_copy	(	const DataType *	vector,
		const LongIndexType	vector_size,
		DataType *	output_vector
	)

static

Normalizes a vector based on Euclidean 2-norm. The result is written into another vector.

Parameters

[in]	vector	Input vector.
[in]	vector_size	Length of the input vector
[out]	output_vector	Output vector, which is the normalization of the input vector.

Returns: 2-norm of the input vector

Definition at line 389 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Norm of vector
     DataType norm = cVectorOperations<DataType>::euclidean_norm(
             vector, vector_size);
  
     // Normalize to output
     DataType scale = 1.0 / norm;
     cVectorOperations<DataType>::copy_scaled_vector(vector, vector_size, scale,
                                                     output_vector);
  
     return norm;
  
     #else
  
     // Norm of vector
     DataType norm = cVectorOperations<DataType>::euclidean_norm(vector,
                                                                 vector_size);
  
     // Normalize to output
     for (LongIndexType i=0; i < vector_size; ++i)
     {
         output_vector[i] = vector[i] / norm;
     }
  
     return norm;
  
     #endif
 }

References cVectorOperations< DataType >::copy_scaled_vector(), and cVectorOperations< DataType >::euclidean_norm().

Referenced by c_golub_kahn_bidiagonalization().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ normalize_vector_in_place()

template<typename DataType >

DataType cVectorOperations< DataType >::normalize_vector_in_place	(	DataType *	vector,
		const LongIndexType	vector_size
	)

static

Normalizes a vector based on Euclidean 2-norm. The result is written in-place.

Parameters

[in,out]	vector	Input vector to be normalized in-place.
[in]	vector_size	Length of the input vector

Returns: 2-Norm of the input vector (before normalization)

Definition at line 338 of file c_vector_operations.cpp.

 {
     #if (USE_CBLAS == 1)
  
     // Norm of vector
     DataType norm = cVectorOperations<DataType>::euclidean_norm(
             vector, vector_size);
  
     // Normalize in place
     DataType scale = 1.0 / norm;
     int incx = 1;
     cblas_interface::xscal(vector_size, scale, vector, incx);
  
     return norm;
  
     #else
  
     // Norm of vector
     DataType norm = cVectorOperations<DataType>::euclidean_norm(vector,
                                                                 vector_size);
  
     // Normalize in place
     for (LongIndexType i=0; i < vector_size; ++i)
     {
         vector[i] /= norm;
     }
  
     return norm;
  
     #endif
 }

References cVectorOperations< DataType >::euclidean_norm().

Referenced by c_golub_kahn_bidiagonalization().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ subtract_scaled_vector()

template<typename DataType >

void cVectorOperations< DataType >::subtract_scaled_vector	(	const DataType *	input_vector,
		const LongIndexType	vector_size,
		const DataType	scale,
		DataType *	output_vector
	)

static

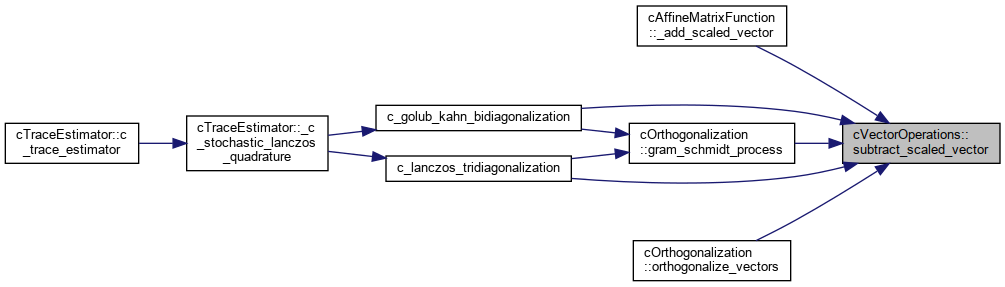
Subtracts the scaled input vector from the output vector.

Performs the following operation:

\[ \boldsymbol{b} = \boldsymbol{b} - c \boldsymbol{a}, \]

where

\( \boldsymbol{a} \) is the input vector,
\( c \) is a scalar scale to the input vector, and
\( \boldsymbol{b} \) is the output vector that is written in-place.

Parameters

[in]	input_vector	A 1D array
[in]	vector_size	Length of vector array
[in]	scale	Scale coefficient to the input vector.
[in,out]	output_vector	Output vector (written in place).

Definition at line 135 of file c_vector_operations.cpp.

 {
  
     #if (USE_CBLAS == 1)
  
     // Using OpenBlas
     int incx = 1;
     int incy = 1;
  
     DataType neg_scale = -scale;
     cblas_interface::xaxpy(vector_size, neg_scale, input_vector, incx,
                            output_vector, incy);
  
     #else
  
     // Not using OpenBlas
     if (scale == 0.0)
     {
         return;
     }
  
     for (LongIndexType i=0; i < vector_size; ++i)
     {
         output_vector[i] -= scale * input_vector[i];
     }
  
     #endif
 }

Referenced by cAffineMatrixFunction< DataType >::_add_scaled_vector(), c_golub_kahn_bidiagonalization(), c_lanczos_tridiagonalization(), cOrthogonalization< DataType >::gram_schmidt_process(), and cOrthogonalization< DataType >::orthogonalize_vectors().

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

/home/runner/work/imate/imate/imate/_c_basic_algebra/c_vector_operations.h
/home/runner/work/imate/imate/imate/_c_basic_algebra/c_vector_operations.cpp

Static Public Member Functions

Detailed Description

template<typename DataType> class cVectorOperations< DataType >

Member Function Documentation

◆ copy_scaled_vector()

◆ copy_vector()

◆ euclidean_norm()

◆ inner_product()

◆ normalize_vector_and_copy()

◆ normalize_vector_in_place()

◆ subtract_scaled_vector()

template<typename DataType>
class cVectorOperations< DataType >