special_functions.h File Reference

#include "../_definitions/types.h"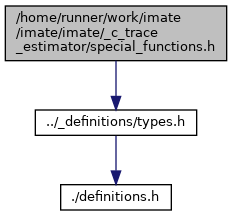

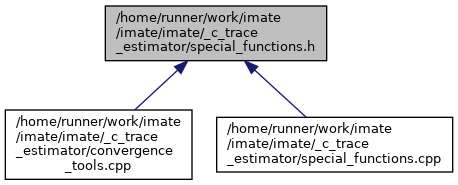
Include dependency graph for special_functions.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
double	erf_inv (const double x)
	Inverse error function. More...

Function Documentation

erf_inv()

double erf_inv

(

const double

x

)

Inverse error function.

The function inverse is found based on Newton method using the evaluation of the error function erf from standard math library and its derivative. The Newton method here uses two refinements.

For further details on the algorithm, refer to: http://www.mimirgames.com/articles/programming/approximations- of-the-inverse-error-function/

The accuracy of this method for the whole input interval of [-1, 1] is in the order of 1e-15 compared to scipy.special.erfinv function.

Parameters

[in]

Input

value, a float number between -1 to 1.

Returns

The inverse error function ranging from -INFINITY to INFINITY.

Definition at line 63 of file special_functions.cpp.

{
    // Output
    double r;
 
    // Check extreme values
    if ((x == 1.0) || (x == -1.0))
    {
        r = sign(x) * INFINITY;
        return r;
    }
 
    double a[4] = {0.886226899, -1.645349621, 0.914624893, -0.140543331};
    double b[5] = {1.0, -2.118377725, 1.442710462, -0.329097515, 0.012229801};
    double c[4] = {-1.970840454, -1.62490649, 3.429567803, 1.641345311};
    double d[3] = {1.0, 3.543889200, 1.637067800};
 
    double z = sign(x) * x;
 
    if (z <= 0.7)
    {
        double x2 = z * z;
        r = z * (((a[3] * x2 + a[2]) * x2 + a[1]) * x2 + a[0]);
        r /= (((b[4] * x2 + b[3]) * x2 + b[2]) * x2 + b[1]) * x2 + b[0];
    }
    else
    {
        double y = sqrt(-log((1.0 - z) / 2.0));
        r = (((c[3] * y + c[2]) * y + c[1]) * y + c[0]);
        r /= ((d[2] * y + d[1]) * y + d[0]);
    }
 
    r = r * sign(x);
    z = z * sign(x);
 
    // These two lines below are identical and repeated for double refinement.
    // Comment one line below for a single refinement of the Newton method.
    r -= (erf(r) - z) / ((2.0 / sqrt(M_PI)) * exp(-r * r));
    r -= (erf(r) - z) / ((2.0 / sqrt(M_PI)) * exp(-r * r));
 
    return r;
}

References sign().

Referenced by ConvergenceTools< DataType >::average_estimates(), and ConvergenceTools< DataType >::check_convergence().

Here is the call graph for this function:

Here is the caller graph for this function: