Data Restoration Settings

The core function within restoreio is restoreio.restore(), which serves a dual purpose: reconstructing incomplete data and generating data ensemble. This section delves into the intricacies of this function for the first application. Alongside this page, you can also explore the comprehensive list of settings available in the API of the restoreio.restore() function.

Time

You can process either the whole or a part of the time span of the input dataset. There are two options available to specify time: single time and time interval.

1. Single Time: Select the time argument to process a specific time within the input dataset. If the chosen time does not exactly match any time stamp in your input data, the closest available time will be used for processing.

2. Time Interval: Alternatively, you can use min_time and max_time arguments to process a specific time interval within the input dataset. If the specified times do not exactly match any time stamps in your input data, the closest available times will be used for processing.

Alternatively, if you do not specify any of the above arguments, the entire time span within your input data will be processed.

Please note that the time interval option cannot be used if you have enabled generating ensemble (refer to the uncertainty_quant argument).

Domain

You have the option to specify a spatial subset of the data for processing using min_lon, max_lon, min_lat, and max_lat argument. By choosing a subset of the domain, the output file will only contain the specified spatial region.

If you do not specify these arguments, the entire spatial extent within your input data will be processed. However, please be aware that for large spatial datasets, this option might require a significant amount of time for processing. To optimize efficiency, we recommend subsetting your input dataset to a relevant segment that aligns with your analysis.

Domain Segmentation

The input dataset’s grid comprises two distinct sets of points: locations with available velocity data and locations where velocity data is not provided. These regions are referred to as the known domain \(\Omega_k\) and the unknown domain \(\Omega_u\), respectively. Therefore, the complete grid of the input data \(\Omega\) can be decomposed into \(\Omega = \Omega_k \cup \Omega_u\).

The primary objective of data reconstruction is to fill the data gaps within the regions where velocity data is missing. The region of missing data, \(\Omega_m\), is part of the unknown domain \(\Omega_u\). However, the unknown domain contains additional points that are not necessarily missing, such as points located on land, denoted as \(\Omega_l\), or regions of the ocean that are not included in the dataset, which we denote as \(\Omega_o\).

Before proceeding with reconstructing the missing velocity data, it is essential to first identify the missing domain \(\Omega_m\). This involves segmenting the unknown domain \(\Omega_u\) into \(\Omega_u = \Omega_m \cup \Omega_l \cup \Omega_o\). These tasks require the knowledge of the ocean’s domain and land domain. You can configure these steps as described in Detect Data Domain and Detect Land below.

For detailed information on domain segmentation, we recommend referring to [1].

Detect Data Domain

By the data domain, \(\Omega_d\), we refer to the union of both the known domain \(\Omega_k\) and the missing domain \(\Omega_m\), namely, \(\Omega_d = \Omega_k \cup \Omega_m\). Once the missing velocity field is reconstructed, the combination of both the known and missing domains will become the data domain. Identifying \(\Omega_d\) can be done in two ways:

1. Using Convex Hull

By enabling the convex_hull option, the data domain \(\Omega_d\) is defined as the region enclosed by a convex hull around the known domain \(\Omega_k\). As such, any unknown point inside the convex hull is flagged as missing, and all points outside this convex hull are considered as part of the ocean domain \(\Omega_o\) or land \(\Omega_l\).

2. Using Concave Hull

By disabling the convex_hull option, the data domain \(\Omega_d\) is defined as the region enclosed by a convex hull around the known domain \(\Omega_k\). As such, any unknown point inside the convex hull is flagged as missing, and all points outside this convex hull are considered as part of the ocean domain \(\Omega_o\) or land \(\Omega_l\).

Note that a concave hull (also known as alpha shape) is not unique and is characterized by a radius parameter. The radius is the inverse of the \(\alpha\) parameter in alpha-shapes. A smaller radius causes the concave hull to shrink more toward the set of points it is encompassing. Conversely, a larger radius yields a concave hull that is closer to a convex hull. We recommend setting the radius (in the unit of Km) to a few multiples of the grid size. For instance, for an HF radar dataset with a 2km resolution, where the grid points are spaced 2 km apart, a radius of approximately 10 km works fine for most datasets.

We recommend choosing concave hull over convex hull as it can better identify the data domain within your input files, provided that the radius parameter is tuned appropriately.

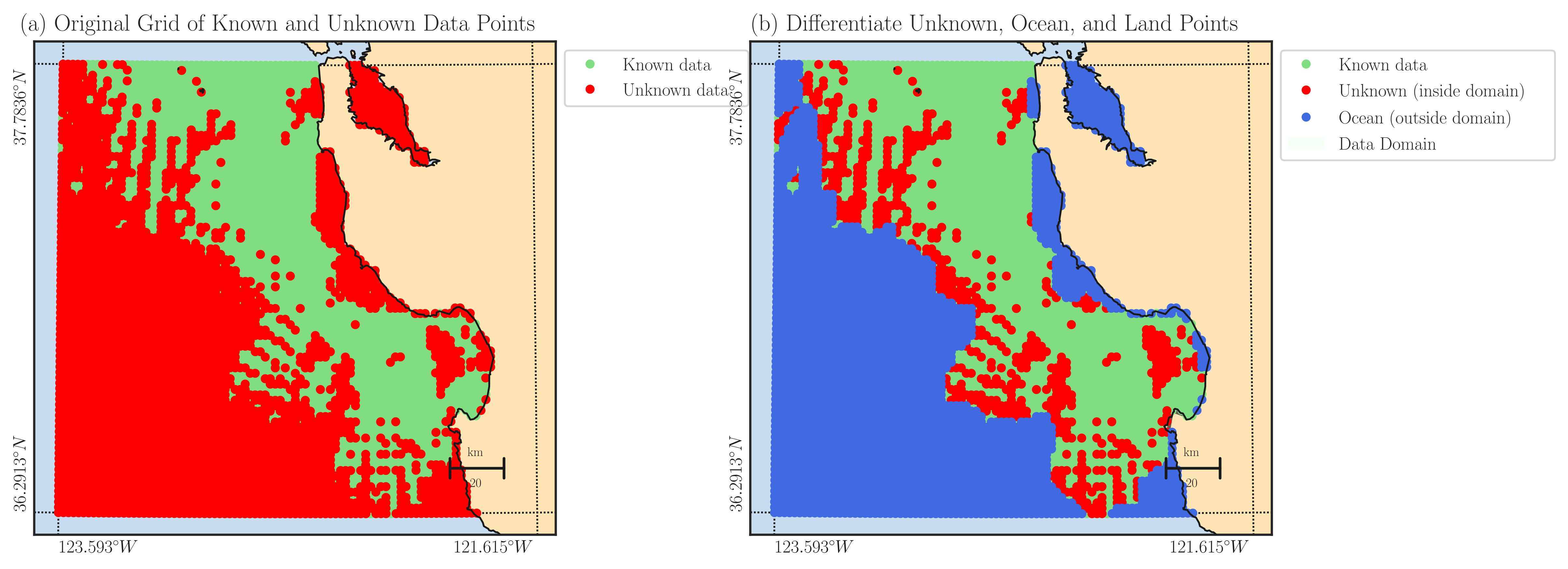
Illustration of Domain Segmentation

The following figure serves as an illustration of the domain segmentation in relation to the provided example code. In the left panel, the green domain represents the known area \(\Omega_k\) where velocity data is available, while the red domain signifies the region \(\Omega_u\) without velocity data. In the right panel, the missing domain \(\Omega_m\) is highlighted in red. This domain is determined by the red points from the left panel that fall within the concave hull around the green points. The points located outside the concave hull are considered non-data points, representing the ocean domain \(\Omega_o\). The restoreio.restore() function reconstructs the velocity field within the red points shown in the right panel.

Detect Land

In some cases, a part of the convex or concave hull might overlap with the land domain, leading to the mistaken flagging of such intersections as missing domains to be reconstructed. To avoid this issue, it is recommended to detect the land domain \(\Omega_l\) and exclude it from the data domain \(\Omega_d\) if there is any intersection. There are three options available regarding the treatment of the land domain:

• Do not detect land, assume all grid is in ocean. This corresponds to setting detect_land option to 0.

• Detect and exclude land (high accuracy, very slow). This correspond to setting detect_land to 1.

• Detect and exclude land. This corresponds to setting detect_land option to 2.

The land boundaries are queried using the Global Self-consistent, Hierarchical, High-resolution Geography Database (GSHHG) . For large datasets, we advise against using the third option, as using high accuracy map can significantly increase the processing time for detecting land. For most datasets, we recommend using the second option, as it offers sufficient accuracy while remaining relatively fast.

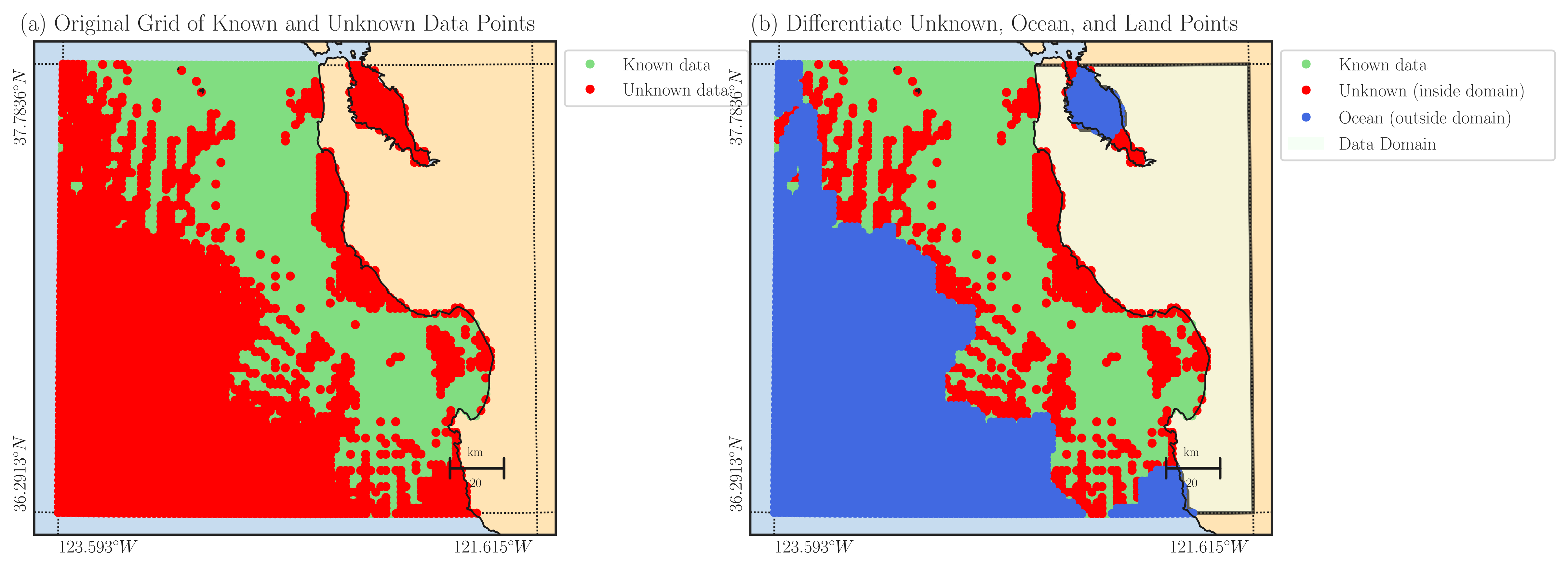
Extend Data Domain to Coastline

If your dataset’s data domain is close to land (e.g., in HF radar datasets spanning across coastlines), you can extend the data domain beyond the region identified by the convex or concave hulls, reaching up to the coastline. To achieve this, you can enable the fill_coast option.

By extending the data domain to the land, a zero boundary condition for the velocity field on the land is imposed. However, it’s important to note that this assumption results in less credible reconstructed fields, especially when dealing with large coastal gaps.

The illustration below showcases the impact of activating the fill_coast feature in the provided example code. Notably, the alteration can be observed in the right panel, where the area between the data domain and the coastline is highlighted in red. This signifies that the gaps extending up to the coastlines will be comprehensively reconstructed.

Refine Grid

With the refine argument, you can increase the dataset’s grid size by an integer factor along both longitude and latitude axes. This process involves interpolating the data onto a more refined grid. It’s important to note that this refinement doesn’t enhance the data resolution.

We advise keeping the refinement level at the default value of 1, unless there’s a specific reason to refine the grid size. Increasing the refinement level can significantly increase computation time and may not provide additional benefits in most cases.