cOrthogonalization< DataType > Class Template Reference

A static class for orthogonalization of vector bases. This class acts as a templated namespace, where all member methods are public and static. More...

#include <c_orthogonalization.h>

Static Public Member Functions
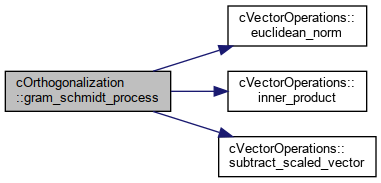
static void	gram_schmidt_process (const DataType *V, const LongIndexType vector_size, const IndexType num_vectors, const IndexType last_vector, const FlagType num_ortho, DataType *r)
	Modified Gram-Schmidt orthogonalization process to orthogonalize the vector v against a subset of the column vectors in the array V. More...
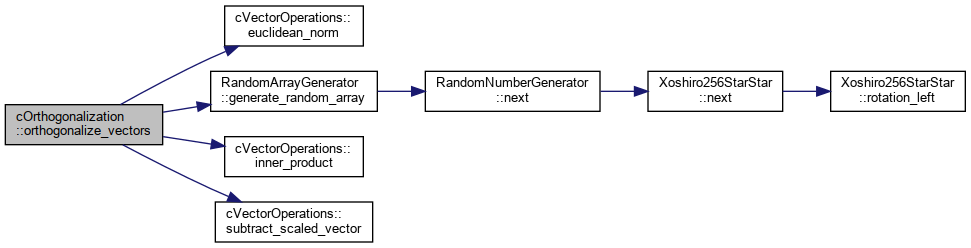
static void	orthogonalize_vectors (DataType *vectors, const LongIndexType vector_size, const IndexType num_vectors)
	Orthogonalizes set of vectors mutually using modified Gram-Schmidt process. More...

Detailed Description

template<typename DataType>
class cOrthogonalization< DataType >

A static class for orthogonalization of vector bases. This class acts as a templated namespace, where all member methods are public and static.

See also

RandomVectors

Definition at line 35 of file c_orthogonalization.h.

Member Function Documentation

gram_schmidt_process()

template<typename DataType >

void cOrthogonalization< DataType >::gram_schmidt_process ( const DataType *  V, const LongIndexType  vector_size, const IndexType  num_vectors, const IndexType  last_vector, const FlagType  num_ortho, DataType *  v  )

static

Modified Gram-Schmidt orthogonalization process to orthogonalize the vector v against a subset of the column vectors in the array V.

V is 1D array of the length vector_size*num_vectors to represent a 2D array of a set of num_vectors column vectors, each of the length vector_size. The length of v is also vector_size.

v is orthogonalized against the last num_ortho columns of V starting from the column vector of the index last_vector. If the backward indexing from last_vector becomes a negative index, the index wraps around from the last column vector index, i.e., num_vectors-1 .

• If num_ortho is zero, or if num_vectors is zero, no orthogonalization is performed.
• If num_ortho is negative (usually set to -1), then v is orthogonalized against all column vectors of V.
• If num_ortho is larger than num_vectors, then v is orthogonalized against all column vectors of V.
• If num_ortho is smaller than num_vectors, then v is orthogonalized against the last num_ortho column vectors of V, starting from the column vector with the index last_vector toward its previous vectors. If the iteration runs into negativen column indices, the column indexing wraps around from the end of the columns from num_vectors-1.

The result of the newer v is written in-place in v.

If vector v is identical to one of the vectors in V, the orthogonalization against the identical vector is skipped.

If one of the column vectors of V is zero (have zero norm), that vector is ignored.

Note

It is assumed that the caller function fills the column vectors of V periodically in a wrapped around order from column index 0,1,... to num_vectors-1, and newer vectors are replaced on the wrapped index starting from index 0,1,... again. Thus, V only stores the last num_vectors column vectors. The index of the last filled vector is indicated by last_vector.

Warning

The vector v can be indeed one of the columns of V itself. However, in this case, vector v must NOT be orthogonalized against itself, rather, it should only be orthogonalized to the other vectors in V. For instance, if num_vectors=10, and v is the 3rd vector of V, and if num_ortho is 6, then we may set last_vector=2. Then v is orthogonalized againts the six columns 2,1,0,9,8,7, where the last three of them are wrapped around the end of the columns.

See also

c_golub_kahn_bidiagonalizaton, c_lanczos_bidiagonalization

Parameters

[in]	V	1D coalesced array of vectors representing a 2D array. The length of this 1D array is vector_size*num_vectors, which indicates a 2D array with the shape (vector_size,num_vectors).
[in]	vector_size	The length of each vector. If we assume V indicates a 2D vector, this is the number of rows of V.
[in]	num_vectors	The number of column vectors. If we assume V indicates a 2D vector, this the number of columns of V.
[in]	last_vector	The column vectors of the array V are rewritten by the caller function in wrapped-around order. That is, once all the columns (from the zeroth to the num_vector-1 vector) are filled, the next vector is rewritten in the place of the zeroth vector, and the indices of newer vectors wrap around the columns of V. Thus, V only retains the last num_vectors vectors. The column index of the last written vector is given by last_vector. This index is a number between 0 and num_vectors-1. The index of the last i-th vector is winding back from the last vector by last_vector-i+1 mod num_vectors.
[in]	num_ortho	The number of vectors to be orthogonalized starting from the last vector. 0 indicates no orthogonalization will be performed and the function just returns. A negative value means all vectors will be orthogonalized. A poisitive value will orthogonalize the given number of vectors. This value cannot be larger than the number of vectors.
[in,out]	v	The vector that will be orthogonalized against the columns of V. The length of v is vector_size. This vector is modified in-place.

Definition at line 125 of file c_orthogonalization.cpp.

{
    // Determine how many previous vectors to orthogonalize against
    IndexType num_steps;
    if ((num_ortho == 0) || (num_vectors < 2))
    {
        // No orthogonalization is performed
        return;
    }
    else if ((num_ortho < 0) ||
             (num_ortho > static_cast<FlagType>(num_vectors)))
    {
        // Orthogonalize against all vectors
        num_steps = num_vectors;
    }
    else
    {
        // Orthogonalize against only the last num_ortho vectors
        num_steps = num_ortho;
    }
 
    // Vectors can be orthogonalized at most to the full basis of the vector
    // space. Thus, num_steps cannot be larger than the dimension of vector
    // space, which is vector_size.
    if (num_steps > static_cast<IndexType>(vector_size))
    {
        num_steps = vector_size;
    }
 
    IndexType i;
    DataType inner_prod;
    DataType norm;
    DataType norm_v;
    DataType epsilon = std::numeric_limits<DataType>::epsilon();
    DataType distance2;
 
    // Iterate over vectors
    for (IndexType step=0; step < num_steps; ++step)
    {
        // i is the index of a column vector in V to orthogonalize v against it
        if ((last_vector % num_vectors) >= step)
        {
            i = (last_vector % num_vectors) - step;
        }
        else
        {
            // Wrap around negative indices from the end of column index
            i = (last_vector % num_vectors) - step + num_vectors;
        }
 
        // Norm of j-th vector
        norm = cVectorOperations<DataType>::euclidean_norm(
                &V[vector_size*i], vector_size);
 
        // Check norm
        if (norm < epsilon * sqrt(vector_size))
        {
            std::cerr << "WARNING: norm of the given vector is too small. " \
                      << "Cannot orthogonalize against zero vector. " \
                      << "Skipping." << std::endl;
            continue;
        }
 
        // Projection
        inner_prod = cVectorOperations<DataType>::inner_product(
                &V[vector_size*i], v, vector_size);
 
        // scale for subtraction
        DataType scale = inner_prod / (norm * norm);
 
        // If scale is 1, it is possible that vector v and j-th vector are
        // identical (or close).
        if (std::abs(std::abs(scale) - 1.0) <= 2.0 * epsilon)
        {
            // Norm of the vector v
            norm_v = cVectorOperations<DataType>::euclidean_norm(
                    v, vector_size);
 
            // Compute distance between the j-th vector and vector v
            distance2 = norm_v*norm_v - 2.0*inner_prod + norm*norm;
 
            // If distance is zero, do not reorthogonalize i-th against
            // the j-th vector.
            if (distance2 < 2.0 * epsilon * vector_size)
            {
                continue;
            }
        }
 
        // Subtraction
        cVectorOperations<DataType>::subtract_scaled_vector(
                &V[vector_size*i], vector_size, scale, v);
    }
}

References cVectorOperations< DataType >::euclidean_norm(), cVectorOperations< DataType >::inner_product(), and cVectorOperations< DataType >::subtract_scaled_vector().

Referenced by c_golub_kahn_bidiagonalization(), and c_lanczos_tridiagonalization().

Here is the call graph for this function:

Here is the caller graph for this function:

orthogonalize_vectors()

template<typename DataType >

void cOrthogonalization< DataType >::orthogonalize_vectors ( DataType *  vectors, const LongIndexType  vector_size, const IndexType  num_vectors  )

static

Orthogonalizes set of vectors mutually using modified Gram-Schmidt process.

Note

Let m be the number of vectors (num_vectors), and let n be the size of each vector (vector_size). In general, n is much larger (large matrix size), and m is small, in order of a couple of hundred. But for small matrices (where n could be smaller then m), then each vector can be orthogonalized at most to n other vectors. This is because the dimension of the vector space is n. Thus, if there are extra vectors, each vector is orthogonalized to window of the previous n vector.

If one of the column vectors is identical to one of other column vectors in V, one of the vectors is regenerated by random array and the orthogonalization is repeated.

Note

If two vectors are identical (or the norm of their difference is very small), they cannot be orthogonalized against each other. In this case, one of the vectors is re-generated by new random numbers.

Warning

if num_vectors is larger than vector_size, the orthogonalization fails since not all vectors are independent, and at least one vector becomes zero.

Parameters

[in,out]	vectors	2D array of size vector_size*num_vectors. This array will be modified in-place and will be output of this function. Note that this is Fortran ordering, meaning that the first index is contiguous. Hence, to call the j-th element of the i-th vector, use &vectors[i*vector_size + j].
[in]	num_vectors	Number of columns of vectors array.
[in]	vector_size	Number of rows of vectors array.

Definition at line 269 of file c_orthogonalization.cpp.

{
    // Do nothing if there is only one vector
    if (num_vectors < 2)
    {
        return;
    }
 
    IndexType i = 0;
    IndexType j;
    IndexType start_j;
    DataType inner_prod;
    DataType norm_j;
    DataType norm_i;
    DataType epsilon = std::numeric_limits<DataType>::epsilon();
    IndexType success = 1;
    IndexType max_num_trials = 20;
    IndexType num_trials = 0;
    IndexType num_threads = 1;
    RandomNumberGenerator random_number_generator(num_threads);
 
    while (i < num_vectors)
    {
        if ((success == 0) && (num_trials >= max_num_trials))
        {
            std::cerr << "ERROR: Cannot orthogonalize vectors after " \
                      << num_trials << " trials. Aborting." \
                      << std::endl;
            abort();
        }
 
        // Reset on new trial (if it was set to 0 before to start a new trial)
        success = 1;
 
        // j iterates on previous vectors in a window of at most vector_size
        if (static_cast<LongIndexType>(i) > vector_size)
        {
            // When vector_size is smaller than i, it is fine to cast to signed
            start_j = i - static_cast<IndexType>(vector_size);
        }
        else
        {
            start_j = 0;
        }
 
        // Reorthogonalize against previous vectors
        for (j=start_j; j < i; ++j)
        {
            // Norm of the j-th vector
            norm_j = cVectorOperations<DataType>::euclidean_norm(
                    &vectors[j*vector_size], vector_size);
 
            // Check norm
            if (norm_j < epsilon * sqrt(vector_size))
            {
                std::cerr << "WARNING: norm of the given vector is too " \
                          << " small. Cannot reorthogonalize against zero" \
                          << "vector. Skipping."
                          << std::endl;
                continue;
            }
 
            // Projecting i-th vector to j-th vector
            inner_prod = cVectorOperations<DataType>::inner_product(
                    &vectors[i*vector_size], &vectors[j*vector_size],
                    vector_size);
 
            // Scale of subtraction
            DataType scale = inner_prod / (norm_j * norm_j);
 
            // Subtraction
            cVectorOperations<DataType>::subtract_scaled_vector(
                    &vectors[vector_size*j], vector_size, scale,
                    &vectors[vector_size*i]);
 
            // Norm of the i-th vector
            norm_i = cVectorOperations<DataType>::euclidean_norm(
                    &vectors[i*vector_size], vector_size);
 
            // If the norm is too small, regenerate the i-th vector randomly
            if (norm_i < epsilon * sqrt(vector_size))
            {
                // Regenerate new random vector for i-th vector
                RandomArrayGenerator<DataType>::generate_random_array(
                        random_number_generator, &vectors[i*vector_size],
                        vector_size, num_threads);
 
                // Repeat the reorthogonalization for i-th vector against
                // all previous vectors again.
                success = 0;
                ++num_trials;
                break;
            }
        }
 
        if (success == 1)
        {
            ++i;
 
            // Reset if num_trials was incremented before.
            num_trials = 0;
        }
    }
}

References cVectorOperations< DataType >::euclidean_norm(), RandomArrayGenerator< DataType >::generate_random_array(), cVectorOperations< DataType >::inner_product(), and cVectorOperations< DataType >::subtract_scaled_vector().

Here is the call graph for this function:

---

The documentation for this class was generated from the following files:

• /home/runner/work/imate/imate/imate/_c_trace_estimator/c_orthogonalization.h
• /home/runner/work/imate/imate/imate/_c_trace_estimator/c_orthogonalization.cpp