Performance on GPU Farm

The performance of imate is tested on multi-GPU devices and the results are compared with the performance on a CPU cluster.

Test Description

The following test computes

(1)\[\mathrm{trace}(\mathbf{A}^{-1}),\]

where \(\mathbf{A}\) is symmetric and positive-definite. The above quantity is a computationally expensive expression that frequently appears in the Jacobian and Hessian of likelihood functions in machine learning.

Algorithm

To compute (1), the stochastic Lanczos quadrature (SLQ) algorithm was employed. The complexity of this algorithm is

(2)\[ \mathcal{O} \left( (\mathrm{nnz}(\mathbf{A}) l + n l^2) s \right),\]

where \(n\) is the matrix size, \(\mathrm{nnz}(\mathbf{A})\) is the number of nonzero elements of the sparse matrix \(\mathbf{A}\), \(l\) is the number of Lanczos iterations, and \(s\) is the number of Monte-Carlo iterations (see details in imate.traceinv(method=’slq’)). The numerical experiment was performed with \(l=80\) and \(s=200\).

Hardware

The computations were carried out on the following hardware:

• For test on CPU: Intel® Xeon CPU E5-2670 v3 with 24 threads.

• For test on GPU: a cluster of eight NVIDIA® GeForce RTX 3090 GPUs and Intel® Xeon Processor (Skylake, IBRS) with 32 threads.

Benchmark Matrices

The table below shows the sparse matrices used in the test, which are chosen from SuiteSparse Matrix Collection and are obtained from real applications. The matrices in the table below are all symmetric positive-definite. The number of nonzero elements (nnz) of these matrices increases approximately by a factor of 5 on average and their sparse density remains at the same order of magnitude (except for the first three).

Matrix Name	Size	nnz	Density	Application
nos5	468	5,172	0.02	Structural Problem
mhd4800b	4,800	27,520	0.001	Electromagnetics
bodyy6	19,366	134,208	0.0003	Structural Problem
G2_circuit	150,102	726,674	0.00003	Circuit Simulation
parabolic_fem	525,825	3,674,625	0.00001	Computational Fluid Dynamics
StocF-1465	1,465,137	21,005,389	0.00001	Computational Fluid Dynamics
Bump_2911	2,911,419	127,729,899	0.00001	Structural Problem
Queen_4147	4,147,110	329,499,284	0.00002	Structural Problem

Arithmetic Types

The benchmark test also examines the performance and accuracy of imate on various arithmetic types of the matrix data. To this end, each of the above matrices was re-cast into 32-bit, 64-bit, and 128-bit floating point types. Depending on the hardware, the followings data types were tested:

• For the test on CPU: 32-bit, 64-bit, and 128-bit floating point data.

• For the test on GPU: 32-bit, 64-bit floating point data.

Note

Supporting 128-bit data types is one of the features of imate, which is often not available in numerical libraries.

Note

NVIDIA CUDA libraries do not support 128-data types.

Scalability with Data Size

The figure below shows the scalability by the relation between the elapsed (wall) time versus the data size.

Here, the data size is measured by the matrix nnz rather than the matrix size. However, the matrix size is indicated by the hollow circle marks in the figure.

• For the test on GPU: 8 GPU devices were used.

• For the test on CPU: 16 CPU threads were used.

Scalability Exponent

Device	Data	\(\alpha\)
CPU	32-bit	1.08
	64-bit	0.89
	128-bit	0.93
GPU	32-bit	0.86
	64-bit	0.92

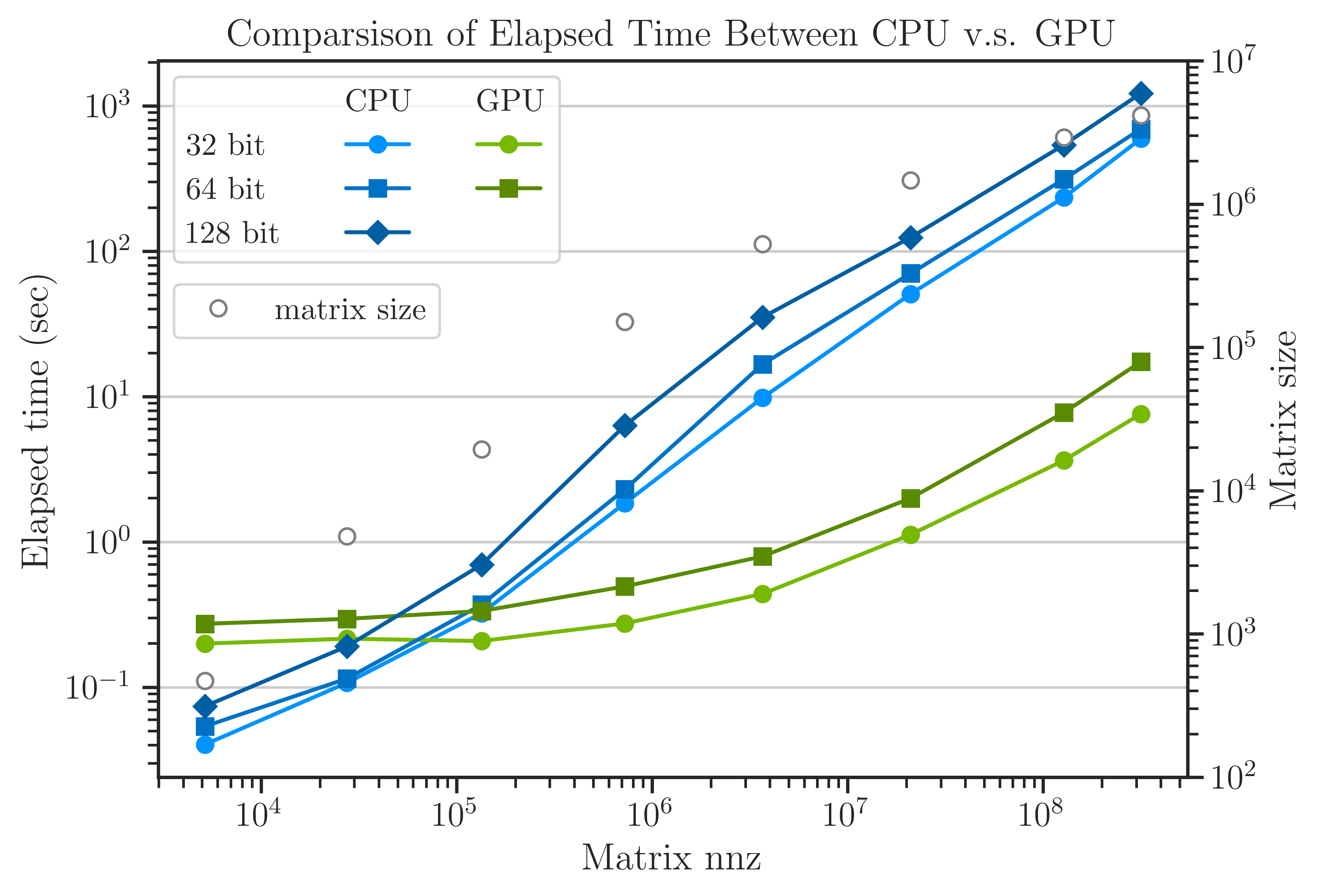
The results show that the computation on GPU is advantageous over CPU when \(\mathrm{nnz}(\mathbf{A}) > 10^{5}\). The empirical complexity can be computed by the relation between the elapsed time \(t\) and the data size by

\[t \propto (\mathrm{nnz}(\mathbf{A}))^{\alpha}.\]

The exponent \(\alpha\) for each experiment at \(\mathrm{nnz}(\mathbf{A}) > 10^{8}\) asymptotically approaches to the values shown in the table below. It can be seen that \(\alpha \approx 1\), which is the theoretical complexity in (2).

Also, the figure implies that processing 32-bit data is at roughly twice faster than 64-bit data on both CPU and GPU, and processing 64-bit data is roughly twice faster than 128-bit on CPU.

Extreme Array Sizes

The above results indicate imate is highly scalable on both CPU and GPU on massive data. However, there are a number of factors that can limit the data size. For instance, the hardware memory limit is one such factor. Another limiting factor is the maximum array length in bits to store the content of a sparse matrix. Interestingly, this factor is not a hardware limitation, rather, is related to the maximum integer (often 32-bit int type) to index the array (in bits) on the memory. The 128-bit format of Queen_4147 matrix is indeed close to such a limit. The above results show that imate is scalable to large scales before reaching such an array size limit.

Beyond Extreme Array Sizes

imate can be configured to handle even larger data (if one can indeed store such an array of data). To do so, increase the integer space for matrix indices by changing UNSIGNED_LONG_INT=1 in /imate/imate/_definitions/definition.h file, or in the terminal set

UNIX

export UNSIGNED_LONG_INT=1

Windows (Powershell)

$env:UNSIGNED_LONG_INT = "1"

Then, recompile imate. See Compile from Source.

Floating Point Arithmetic Accuracy

The advantage of the 32-bit data type in faster processing comes with the cost of higher arithmetic errors. While such errors are negligible for small data, they can be significant for larger data sizes. To examine this, the results of 32-bit and 64-bit data were compared with the result of 128-bit as the benchmark. The figure below shows that both 32-bit and 64-bit data have less than \(0.1 \%\) error relative to 128-bit data. However, for data size larger than \(10^{7}\), the error of 32-bit data reaches \(30 \%\) relative to 128-bit data whereas the 64-bit data maintain \(0.1 \sim 1 \%\) error. Because of this, 64-bit data is often considered for scientific computing since it balances accuracy and speed.

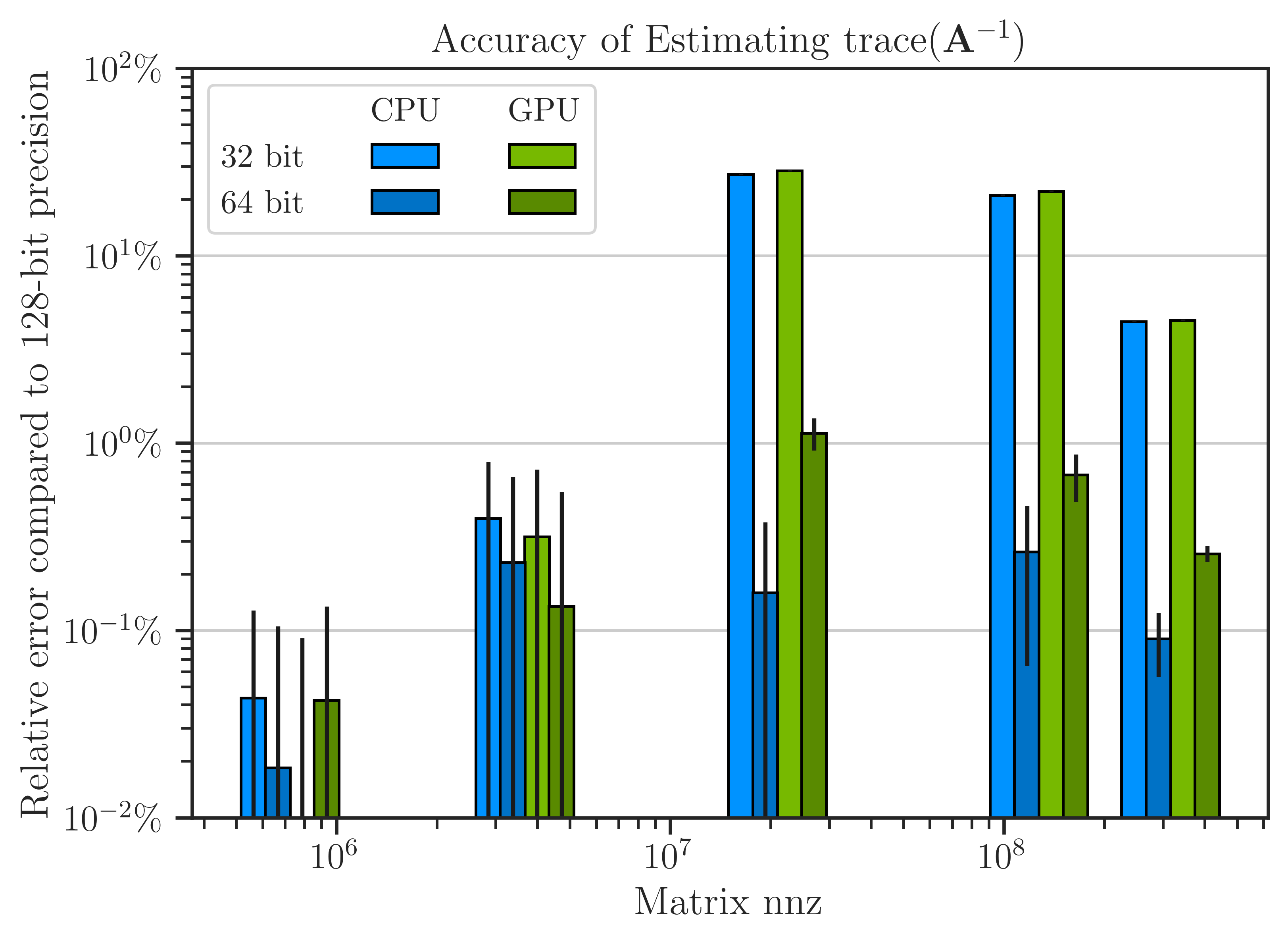
Note that the results of the SLQ method, as a randomized algorithm, is not deterministic. To eliminate the stochastic outcomes as much as possible, the experiments were repeated ten times and the results were averaged. The standard deviation of the results are shown by the error bars in the figure.

Scalability with Increase of GPU Devices

Another method to examine the scalability of imate is to observe the performance by the increase of the number of CPU threads or GPU devices as shown in the figure below.

Scalability Exponent

Device	Data	\(\beta\)
CPU	32-bit	0.83
	64-bit	0.80
	128-bit	0.76
GPU	32-bit	0.98
	64-bit	0.96

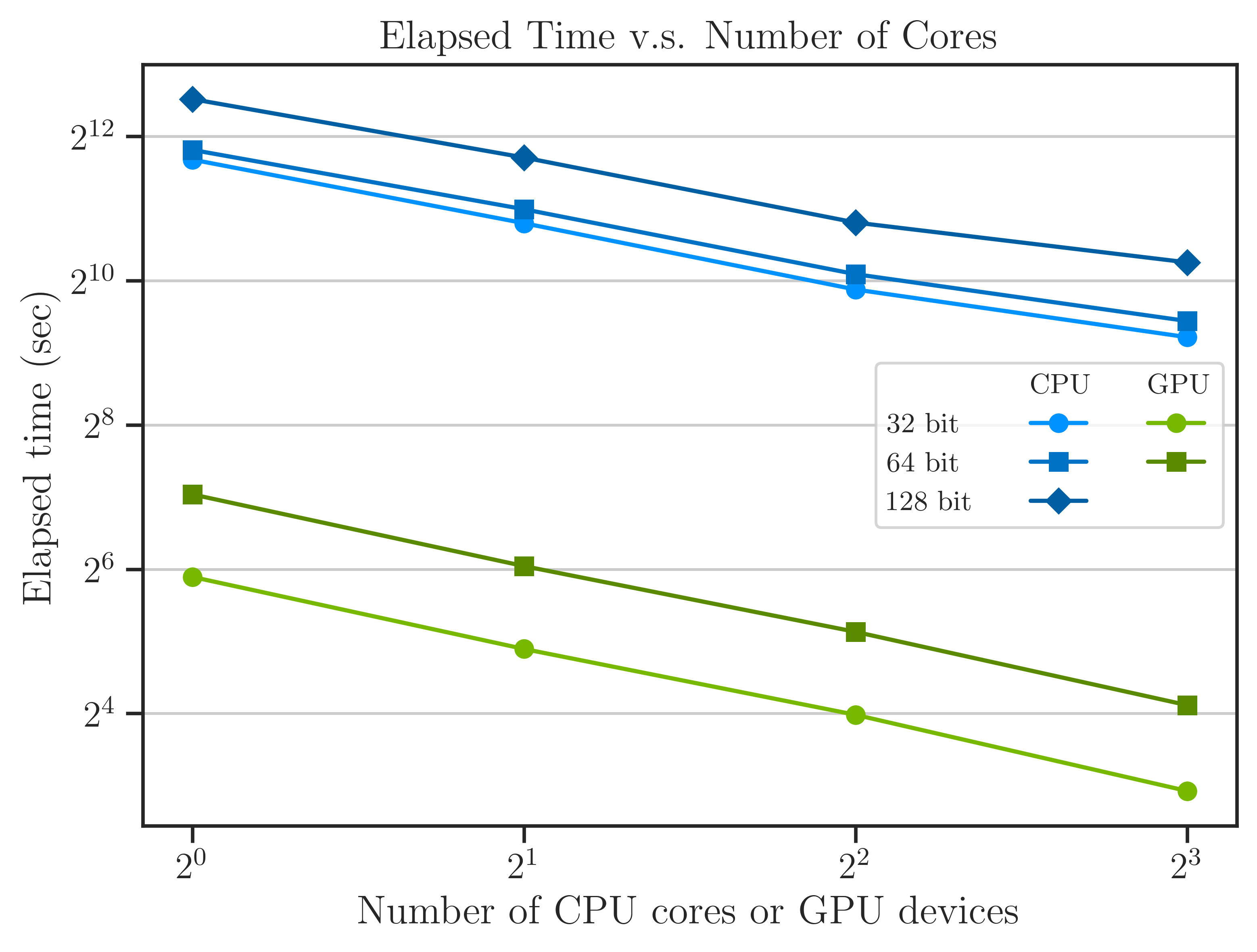
The above results correspond to the largest matrix in the test, namely Queen_4147. The performance on GPUs is over thirty-fold faster than the CPU for the same number of threads and GPU devices, although, this may not be a fair comparison. However, the performance of only one GPU device is yet five times faster than 8 CPU threads. Note that the elapsed time includes the data transfer between host and GPU device which is significantly slower than the data transfer between shared memory of the CPU cluster. Despite this, the overall performance on GPU is yet remarkably faster.

The scalability can be quantified by relating the elapsed (wall) time, \(t\), and the number of computing components \(m\) (CPU threads or GPU devices) by

\[t \propto \frac{1}{m^{\beta}}.\]

The estimated values of \(\beta\) from the curves in the figure are shown in the table below, which implies the GPU test achieves better scalability. Moreover, The speed (inverse of elapsed time) per CPU thread tends to saturate with the increase in the number of CPU threads. In contrast, the GPU results maintain the linear behavior by the increase in the number of GPU devices.

How to Reproduce Results

Prepare Matrix Data

1. Download all the above-mentioned sparse matrices from SuiteSparse Matrix Collection. For instance, download Queen_4147.mat from Queen_4147.

2. Run /imate/benchmark/matrices/read_matrix.m to extract sparse matrix data from Queen_4147.mat:

   read_matrix('Queen_4147.mat');
   

3. Run /imate/benchmark/matrices/read_matrix.py to convert the outputs of the above Octave script to generate a python pickle file:

   read_matrix.py Queen_4147 float32    # to generate 32-bit data
   read_matrix.py Queen_4147 float64    # to generate 64-bit data
   read_matrix.py Queen_4147 float128   # to generate 128-bit data
   

   The output of the above script will be written in /imate/benchmark/matrices/.

Perform Numerical Test

Run /imate/benchmark/scripts/benchmark_speed.py to read the matrices and generate results. The output of this script is written to /imate/benchmark/pickle_results as a pickle file.

Run Locally

• For the CPU test, run:

  cd /imate/benchmark/scripts
  python ./benchmark_speed.py -c
  

• For the GPU test:

  cd /imate/benchmark/scripts
  python ./benchmark_speed.py -g
  

Submit Job to Cluster with SLURM

• Submit the job file /imate/benchmark/jobfiles/jobfile_benchmark_speed_cpu.sh to perform the CPU test by

  cd /imate/benchmark/jobfiles
  sbatch jobfile_benchmark_speed_cpu.sh
  

• Submit the job file /imate/benchmark/jobfiles/jobfile_benchmark_speed_gpu.sh to perform the GPU test by

  cd /imate/benchmark/jobfiles
  sbatch jobfile_benchmark_speed_gpu.sh
  

Plot Results

Run /imate/benchmark/notebooks/plot_benchmark_speed.ipynb to generate plots shown in the above from the pickled results. This notebook stores plots as svg files in /imate/benchmark/svg_plots/.