Comparison of Performance with and without OpenBLAS#

Almost all computational software are built upon existing numerical libraries for basic linear algebraic subprograms (BLAS), such as BLAS, OpenBLAS, NVIDIA® cuBLAS, NVIDIA® cuSparse, and Intel® Math Kernel Library, to name a few. imate uses cuBLAS and cuSparse for basic vector and matrix operations on GPU devices. However, for computation on CPU, imate comes with its own library for basic numerical operations for vector and matrix operations, which supports both dense and sparse matrices. Despite this, imate can also be compiled with OpenBLAS instead of its own library.

Note

OpenBLAS library has three levels of functionalities: levels one, two, and three, respectively for vector-vector, matrix-vector, and matrix-matrix operations. OpenBLAS, however, only supports operations on dense matrices. As such, when imate is compiled with OpenBLAS, it only uses level one functionalities of OpenBLAS for sparse data. For level two and three operations, imate uses its own library.

The following numerical experiment compares the performance and accuracy of imate with and without using OpenBLAS.

Test Description#

In the following numerical experiments, the goal is to compute

(1)#\[\mathrm{trace}(\mathbf{A}^{-1}),\]

where \(\mathbf{A}\) is symmetric and positive-definite. The above quantity is a computationally expensive expression that frequently appears in the Jacobian and Hessian of likelihood functions in machine learning.

Algorithm#

To compute (1), the stochastic Lanczos quadrature (SLQ) algorithm is employed. The complexity of this algorithm is

(2)#\[ \mathcal{O} \left( (\mathrm{nnz}(\mathbf{A}) l + n l^2) s \right),\]

where \(n\) is the matrix size, \(\mathrm{nnz}(\mathbf{A})\) is the number of nonzero elements of the sparse matrix \(\mathbf{A}\), \(l\) is the number of Lanczos iterations, and \(s\) is the number of Monte-Carlo iterations (see details in imate.traceinv(method=’slq’)). The numerical experiment is performed with \(l=80\) and \(s=200\). The computations were carried out on Intel® Xeon CPU E5-2670 v3 with 24 threads.

Arithmetic Types#

The benchmark test also examines the performance and accuracy of imate on various arithmetic types of the matrix data. To this end, the matrices that are described below are re-cast into 32-bit, 64-bit, and 128-bit floating point types.

Note

Supporting 128-bit data types is one of the features of imate, which is often not available in numerical libraries, such as OpenBLAS.

Test on Dense Matrices#

The Gramian matrix \(\mathbf{A} = \mathbf{B}^{\intercal} \mathbf{B}\) is considered for the test where \(\mathbf{B}\) is a bi-diagonal Toeplitz matrix defined by

\[\begin{split}B_{ij} = \begin{cases} a, & i = j, \\ b, & i+1 = j. \end{cases}\end{split}\]

The above matrix can be generated by imate.toeplitz() function. In this experiment, \(a = 2\), \(b = 1\), and the matrix size is varied by powers of two, \(n = 2^8, 2^9, \dots, 2^{14}\).

An advantage of using the above matrix is that an analytic formula for (1) for \(n \gg 1\) is known by

(3)#\[ \mathrm{trace}(\mathbf{A}^{-1}) \approx \frac{1}{a^2 - b^2} \left( n - \frac{q^{2}}{1 - q^2} \right),\]

where \(q = b/a\). See imate.sample_matrices.toeplitz_traceinv() for details. The above analytic formula is used as the benchmark solution to test the accuracy of the results.

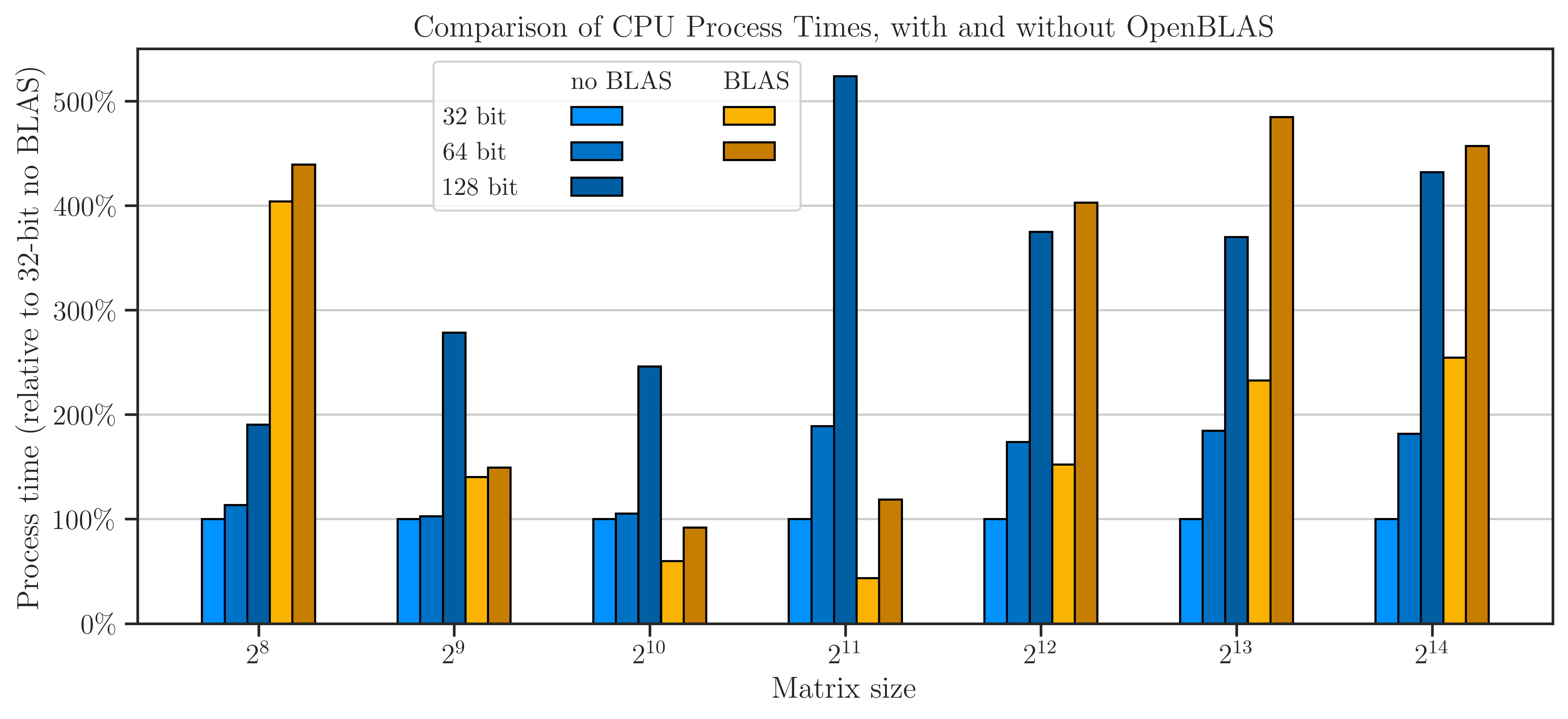
Process Time#

The processing time of the computations is shown in the figure below. The speed of computation with and without using OpenBLAS for \(n < 10^{12}\) shows mixed results. However, at \(n \geq 2^{12}\), the speed of computation without using OpenBLAS is consistently superior by a factor of roughly 1.5 to 2.5.

../_images/benchmark_openblas_dense_time.png

Floating Point Arithmetic Accuracy#

The accuracy of floating point arithmetic is compared with and without using OpenBLAS in the next figure. The error is obtained by comparing the results with (3) as the benchmark. The figure implies that the results of both 32-bit and 64-bit data types with and without openBLAS are almost insignificant.

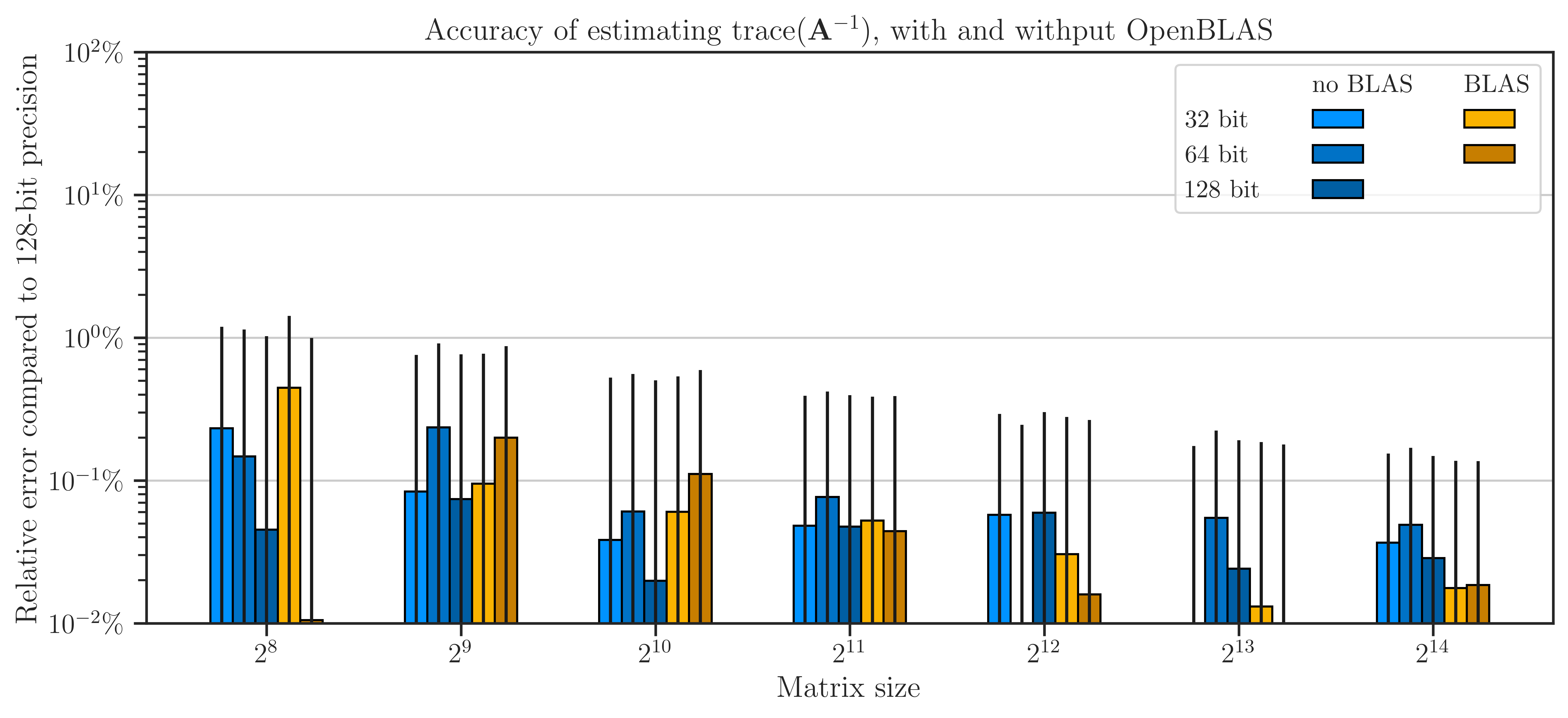
../_images/benchmark_openblas_dense_accuracy.png

Recall that the SLQ method is a randomized algorithm, hence, the results are not deterministic. To diminish the effect of the randomness of the algorithm, the numerical experiment is repeated ten times. The standard deviation of the results is shown by the error bars in the figure. However, the values of the plot itself are not the average of the results, rather, only the result of one of the repeats is shown in order to demonstrate the error after 200 Monte-Carlo iterations (and not 10 times 200 iterations).

Test on Sparse Matrices#

As noted above, OpenBLAS only supports dense matrices. However, imate can yet utilize level one functions of OpenBLAS for sparse matrices. The following examines the performance on sparse matrices.

The table below shows the sparse matrices used in the test, which are chosen from SuiteSparse Matrix Collection and are obtained from real applications. The matrices in the table below are all symmetric positive-definite. The number of nonzero elements (nnz) of these matrices increases approximately by a factor of 5 on average and their sparse density remains at the same order of magnitude (except for the first three).

Matrix Name	Size	nnz	Density	Application
`nos5`	468	5,172	0.02	Structural Problem
`mhd4800b`	4,800	27,520	0.001	Electromagnetics
`bodyy6`	19,366	134,208	0.0003	Structural Problem
`G2_circuit`	150,102	726,674	0.00003	Circuit Simulation
`parabolic_fem`	525,825	3,674,625	0.00001	Computational Fluid Dynamics
`StocF-1465`	1,465,137	21,005,389	0.00001	Computational Fluid Dynamics
`Bump_2911`	2,911,419	127,729,899	0.00001	Structural Problem
`Queen_4147`	4,147,110	329,499,284	0.00002	Structural Problem

Floating Point Arithmetic Accuracy#

The accuracy of floating point arithmetic is compared with and without using OpenBLAS in the next figure. The error is obtained by comparing the results with the computation on 128-bit data type without using OpenBLAS as the benchmark. The figure implies that the results of both 32-bit and 64-bit data types with and without openBLAS are almost insignificant at \(\mathrm{nnz}(\mathbf{A}) < 10^7\) or for 32-bit data types. In contrast, for larger matrices and 64-bit data type, the imate library without OpenBLAS significantly produces less arithmetic error compared with OpenBLAS.

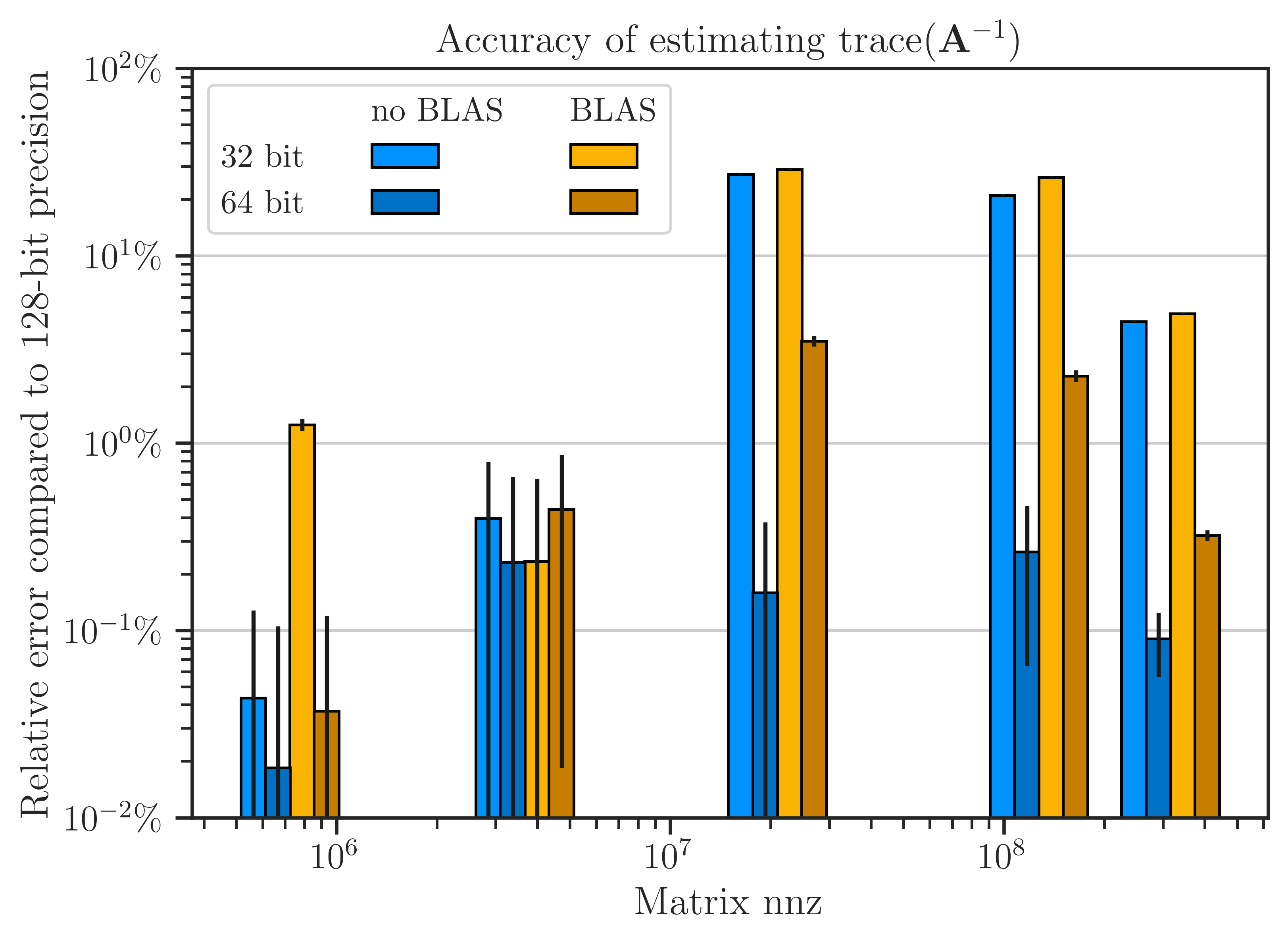
../_images/benchmark_openblas_sparse_accuracy.png

Why imate Has Better Arithmetic Accuracy?#

The difference in arithmetic error between OpenBLAS and imate is surprisingly simple and is related to how the sum-reduction operation

\[c \gets \sum_{i=1}^n a_i b_i,\]

is implemented. In OpenBLAS (and several other BLAS-type libraries), the type of the summation variable \(c\) is the same as the type of input variables \(a_i\) and \(b_i\). In contrast, in imate, the type of \(c\) is always 128-bit (see table below), and once the sum-reduction operation is done, \(c\) is cast down to the type of \(a_i\) and \(b_i\).

When \(a_i\) and \(b_i\) is 32-bit, the effect of the above resolution is negligible compared to large arithmetic errors of 32-bit type. However, for 64-bit data, which has smaller arithmetic errors, the effect of the above resolution is noticeable as shown by the above figure.

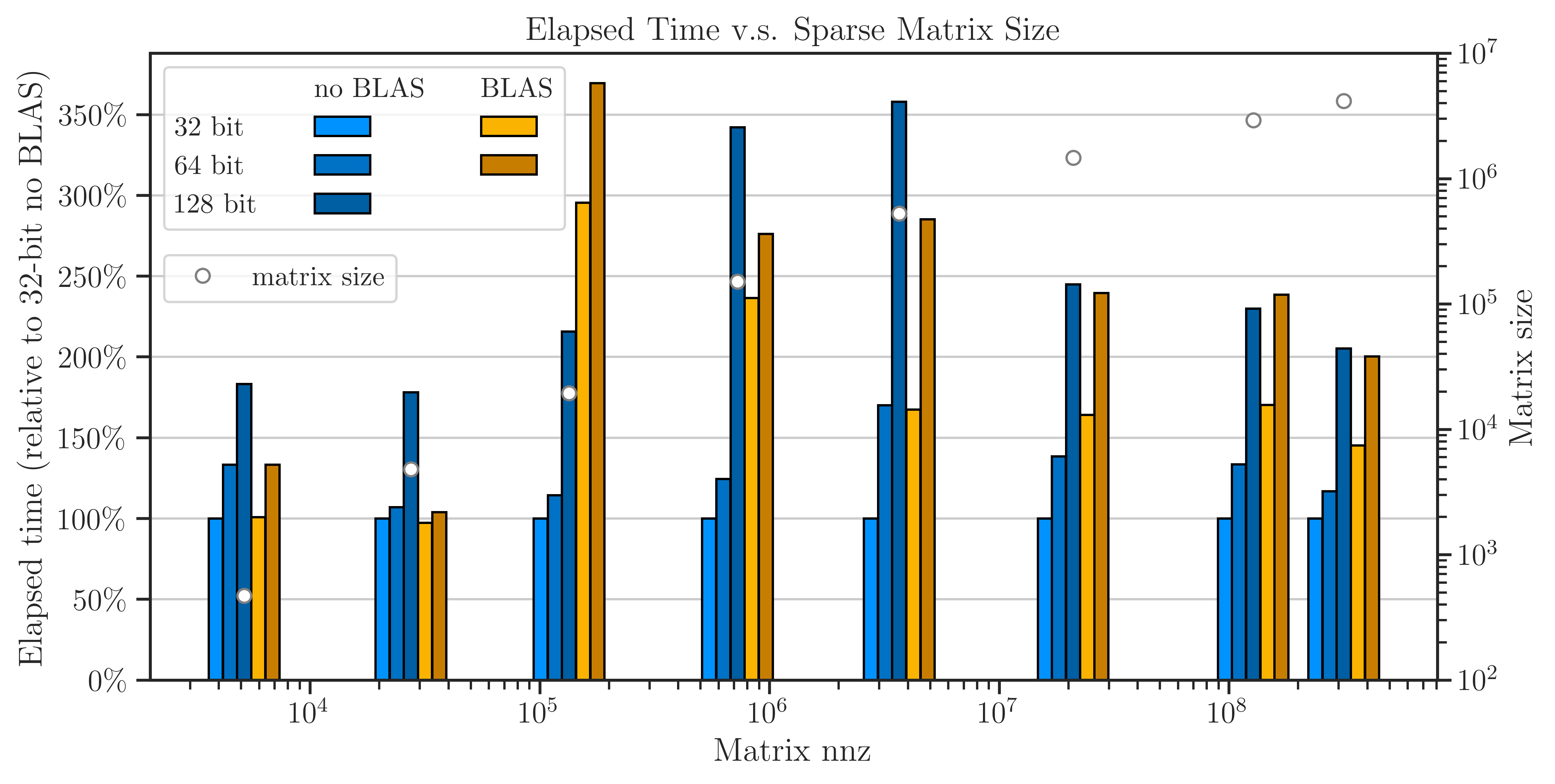
Elapsed Time#

The figure below shows the elapsed (wall) time of the computation. For small matrices, \(\mathrm{nnz}(\mathbf{A}) < 10^{5}\), the results with and without OpenBLAS are comparable. However, for larger matrices, there is a significant difference between the two experiments where OpenBLAS is consistently slower than the built-in imate library by a factor of at least two.

../_images/benchmark_openblas_sparse_time.png

Scalability with CPU Cores#

The scalability of computation is shown in the figure below by the elapsed time versus the number of CPU cores. OpenBLAS is less scalable as the curves in the figure saturate (depart from the linear behavior) more quickly compared to no OpenBLAS.

../_images/benchmark_openblas_sparse_cores.png

How to Reproduce Results#

Prepare Matrix Data#

Download all the above-mentioned sparse matrices from SuiteSparse Matrix Collection. For instance, download Queen_4147.mat from Queen_4147.
Run /imate/benchmark/matrices/read_matrix.m to extract sparse matrix data from Queen_4147.mat:
```
read_matrix('Queen_4147.mat');
```

Run /imate/benchmark/matrices/read_matrix.py to convert the outputs of the above script to generate a python pickle file:

read_matrix.py Queen_4147 float32    # to generate 32-bit data
read_matrix.py Queen_4147 float64    # to generate 64-bit data
read_matrix.py Queen_4147 float128   # to generate 128-bit data

The output of the above script will be written in /imate/benchmark/matrices/.

Perform Numerical Test#

Run each of the scripts described below with and without using OpenBLAS support in imate to compare their performance. The default installation of imate (if you installed it with pip or cond) does not come with OpenBLAS support. To use OpenBLAS, imate has to be compiled from the source.

Tip

To compile imate using OpenBLAS, export the environment variable:

export USE_CBLAS=1

or set USE_CBLAS=1 in /imate/_definitions/definition.h. By default, USE_CBLAS is set to 0. Then, recompile imate. See Compile from Source.

Dense Matrices, Run Locally#

Run /imate/benchmark/scripts/benchmark_openblas_dense.py as follows:

To reproduce the results without OpenBLAS:

cd /imate/benchmark/scripts
python ./benchmark_openblas_dense.py -o False

To reproduce the results with OpenBLAS, first, compile imate with OpenBLAS (see above), then run:
```
cd /imate/benchmark/scripts
python ./benchmark_openblas_dense.py -o True
```

Dense Matrices, Submit to Cluster with SLURM#

Submit the job file /imate/benchmark/jobfiles/jobfile_benchmark_openblas_dense.sh by

cd /imate/benchmark/jobfiles
sbatch jobfile_benchmark_openblas_dense.sh

To use with or without OpenBLAS, modify the above job files (uncomment lines the corresponding).

Sparse Matrices, Run Locally#

Run /imate/benchmark/scripts/benchmark_speed.py script as follows:

cd /imate/benchmark/scripts
python ./benchmark_speed.py -c

Sparse Matrices, Submit to Cluster with SLURM#

Submit the job file /imate/benchmark/jobfiles/jobfile_benchmark_speed_cpu.sh by

cd /imate/benchmark/jobfiles
sbatch jobfile_benchmark_speed_cpu.sh

Plot Results#

Run /imate/benchmark/notebooks/plot_benchmark_openblas_dense.ipynb to generate plots for the dense matrices shown in the above
Run /imate/benchmark/notebooks/plot_benchmark_openblas_sparse.ipynb to generate plots for the sparse matrices shown in the above

These notebooks stores the plots as svg files in /imate/benchmark/svg_plots/.