c_golub_kahn_bidiagonalization.h File Reference

#include "../_c_linear_operator/c_linear_operator.h"
#include "../_definitions/types.h"

Include dependency graph for c_golub_kahn_bidiagonalization.h:

This graph shows which files directly or indirectly include this file:

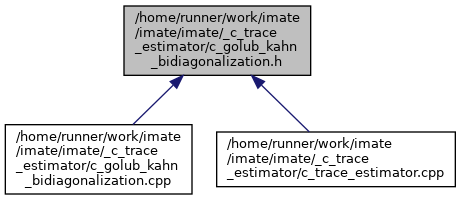
Go to the source code of this file.

Functions
template<typename DataType >
IndexType	c_golub_kahn_bidiagonalization (cLinearOperator< DataType > *A, const DataType *v, const LongIndexType n, const IndexType m, const DataType lanczos_tol, const FlagType orthogonalize, DataType *alpha, DataType *beta)
	Bi-diagonalizes the positive-definite matrix A using Golub-Kahn-Lanczos method. More...

Function Documentation

c_golub_kahn_bidiagonalization()

template<typename DataType >

IndexType c_golub_kahn_bidiagonalization	(	cLinearOperator< DataType > *	A,
		const DataType *	v,
		const LongIndexType	n,
		const IndexType	m,
		const DataType	lanczos_tol,
		const FlagType	orthogonalize,
		DataType *	alpha,
		DataType *	beta
	)

Bi-diagonalizes the positive-definite matrix A using Golub-Kahn-Lanczos method.

This method bi-diagonalizes matrix A to B using the start vector w. m is the Lanczos degree, which will be the size of square matrix B.

The output of this function are alpha (of length m) and beta (of length m+1) which are diagonal (alpha[:]) and off-diagonal (beta[1:]) elements of the bi-diagonal (m,m) symmetric and positive-definite matrix B.

Lanczos tridiagonalization vs Golub-Kahn Bidiagonalization

• The Lanczos tri-diagonalization is twice faster (in runtime), as it has only one matrix-vector multiplication. Whereas the Golub-Kahn bi-diagonalization has two matrix-vector multiplications.
• The Lanczos tri-diagonalization can only be applied to symmetric matrices. Whereas the Golub-Kahn bi-diagonalization can be applied to any matrix.

Reference

• NetLib Algorithm 6.27, netlib.org/utk/people/JackDongarra/etemplates/node198.html
• Matrix Computations, Golub, p. 495
• Demmel, J., Templates for Solution of Algebraic Eigenvalue Problem, p. 143

Warning

When the matrix A is very close to the identity matrix, the Golub-Kahn bi-diagonalization method can not find beta, as beta becomes zero. If A is not exactly identity, you may decrease the Tolerance to a very small number. However, if A is almost identity matrix, decreasing lanczos_tol will not help, and this function cannot be used.

See also

lanczos_tridiagonalizaton

Parameters

[in]	A	A linear operator that represents a matrix of size (n,n) and can perform matrix-vector operation with dot() method and transposed matrix-vector operation with transpose_dot() method. This matrix should be positive-definite.
[in]	v	Start vector for the Lanczos tri-diagonalization. Column vector of size n. It could be generated randomly. Often it is generated by the Rademacher distribution with entries +1 and -1.
[in]	n	Size of the square matrix A, which is also the size of the vector v.
[in]	m	Lanczos degree, which is the number of Lanczos iterations.
[in]	lanczos_tol	The tolerance of the residual error of the Lanczos iteration.
[in]	orthogonalize	Indicates whether to orthogonalize the orthogonal eigenvectors during Lanczos recursive iterations. If set to 0, no orthogonalization is performed. If set to a negative integer, a newly computed eigenvector is orthogonalized against all the previous eigenvectors (full reorthogonalization). If set to a positive integer, say q less than lanczos_degree, the newly computed eigenvector is orthogonalized against the last q previous eigenvectors (partial reorthogonalization). If set to an integer larger than lanczos_degree, it is cut to lanczos_degree, which effectively orthogonalizes against all previous eigenvectors (full reorthogonalization).
[out]	alpha	This is a 1D array of size m and alpha[:] constitute the diagonal elements of the bi-diagonal matrix B. This is the output and written in place.
[out]	beta	This is a 1D array of size m, and the elements beta[:] constitute the sup-diagonals of the bi-diagonal matrix B. This array is the output and written in place.

Returns

Counter for the Lanczos iterations. Normally, the size of the output matrix should be (m,m), which is the Lanczos degree. However, if the algorithm terminates early, the size of alpha and beta, and hence the output tri-diagonal matrix, is smaller. This counter keeps track of the non-zero size of alpha and beta.

Definition at line 111 of file c_golub_kahn_bidiagonalization.cpp.

{
    // buffer_size is number of last orthogonal vectors to keep in buffers U, V
    IndexType buffer_size;
    if (orthogonalize == 0)
    {
        // At least two vectors must be stored in buffer for Lanczos recursion
        buffer_size = 2;
    }
    else if ((orthogonalize < 0) ||
             (orthogonalize > static_cast<FlagType>(m) - 1))
    {
        // Using full reorthogonalization, keep all of the m vectors in buffer
        buffer_size = m;
    }
    else
    {
        // Orthogonalize with less than m vectors (0 < orthogonalize < m-1)
        // plus one vector for the latest (the j-th) vector
        buffer_size = orthogonalize + 1;
    }
 
    // Allocate 2D array (as 1D array, and coalesced row-wise) to store
    // the last buffer_size of orthogonalized vectors of length n. New vectors
    // are stored by cycling through the buffer to replace with old ones.
    DataType* U = new DataType[n * buffer_size];
    DataType* V = new DataType[n * buffer_size];
 
    // Normalize vector v and copy to v_old
    cVectorOperations<DataType>::normalize_vector_and_copy(v, n, &V[0]);
 
    // Declare iterators
    IndexType j;
    IndexType lanczos_size = 0;
    IndexType num_ortho;
 
    // Golub-Kahn iteration
    for (j=0; j < m; ++j)
    {
        // Counter for the non-zero size of alpha and beta
        ++lanczos_size;
 
        // u_new = A.dot(v_old)
        A->dot(&V[(j % buffer_size)*n], &U[(j % buffer_size)*n]);
 
        // Performing: u_new[i] = u_new[i] - beta[j] * u_old[i]
        if (j > 0)
        {
            cVectorOperations<DataType>::subtract_scaled_vector(
                    &U[((j-1) % buffer_size)*n], n, beta[j-1],
                    &U[(j % buffer_size)*n]);
        }
 
        // orthogonalize u_new against previous vectors
        if (orthogonalize != 0)
        {
            // Find how many column vectors are filled so far in the buffer V
            if (j < buffer_size)
            {
                num_ortho = j;
            }
            else
            {
                num_ortho = buffer_size - 1;
            }
 
            // Gram-Schmidt process
            if (j > 0)
            {
                cOrthogonalization<DataType>::gram_schmidt_process(
                        &U[0], n, buffer_size, (j-1)%buffer_size, num_ortho,
                        &U[(j % buffer_size)*n]);
            }
        }
 
        // Normalize u_new and set its norm to alpha[j]
        alpha[j] = cVectorOperations<DataType>::normalize_vector_in_place(
                &U[(j % buffer_size)*n], n);
 
        // Performing: v_new = A.T.dot(u_new) - alpha[j] * v_old
        A->transpose_dot(&U[(j % buffer_size)*n], &V[((j+1) % buffer_size)*n]);
 
        // Performing: v_new[i] = v_new[i] - alpha[j] * v_old[i]
        cVectorOperations<DataType>::subtract_scaled_vector(
                &V[(j % buffer_size)*n], n, alpha[j],
                &V[((j+1) % buffer_size)*n]);
 
        // orthogonalize v_new against previous vectors
        if (orthogonalize != 0)
        {
            cOrthogonalization<DataType>::gram_schmidt_process(
                    &V[0], n, buffer_size, j%buffer_size, num_ortho,
                    &V[((j+1) % buffer_size)*n]);
        }
 
        // Update beta as the norm of v_new
        beta[j] = cVectorOperations<DataType>::normalize_vector_in_place(
                &V[((j+1) % buffer_size)*n], n);
 
        // Exit criterion when the vector r is zero. If each component of a
        // zero vector has the tolerance epsilon, (which is called lanczos_tol
        // here), the tolerance of norm of r is epsilon times sqrt of n.
        if (beta[j] < lanczos_tol * sqrt(n))
        {
            break;
        }
    }
 
    // Free dynamic memory
    delete[] U;
    delete[] V;
 
    return lanczos_size;
}

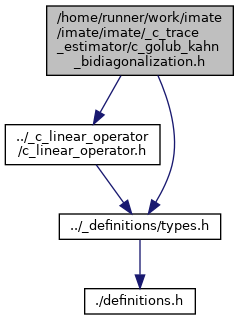
References cLinearOperator< DataType >::dot(), cOrthogonalization< DataType >::gram_schmidt_process(), cVectorOperations< DataType >::normalize_vector_and_copy(), cVectorOperations< DataType >::normalize_vector_in_place(), cVectorOperations< DataType >::subtract_scaled_vector(), and cLinearOperator< DataType >::transpose_dot().

Referenced by cTraceEstimator< DataType >::_c_stochastic_lanczos_quadrature().

Here is the call graph for this function:

Here is the caller graph for this function: