#include "./c_lanczos_tridiagonalization.h"
#include <cmath>
#include "./c_orthogonalization.h"
#include "../_c_basic_algebra/c_vector_operations.h"

Include dependency graph for c_lanczos_tridiagonalization.cpp:

Functions
template<typename DataType >
IndexType	c_lanczos_tridiagonalization (cLinearOperator< DataType > A, const DataType v, const LongIndexType n, const IndexType m, const DataType lanczos_tol, const FlagType orthogonalize, DataType alpha, DataType beta)
	Tri-diagonalizes matrix `A` to `T` using the start vector `v`. `is` the Lanczos degree, which will be the size of square matrix `T`. More...

template IndexType	c_lanczos_tridiagonalization< float > (cLinearOperator< float > A, const float v, const LongIndexType n, const IndexType m, const float lanczos_tol, const FlagType orthogonalize, float alpha, float beta)

template IndexType	c_lanczos_tridiagonalization< double > (cLinearOperator< double > A, const double v, const LongIndexType n, const IndexType m, const double lanczos_tol, const FlagType orthogonalize, double alpha, double beta)

template IndexType	c_lanczos_tridiagonalization< long double > (cLinearOperator< long double > A, const long double v, const LongIndexType n, const IndexType m, const long double lanczos_tol, const FlagType orthogonalize, long double alpha, long double beta)

Function Documentation

◆ c_lanczos_tridiagonalization()

template<typename DataType >

IndexType c_lanczos_tridiagonalization	(	cLinearOperator< DataType > *	A,
		const DataType *	v,
		const LongIndexType	n,
		const IndexType	m,
		const DataType	lanczos_tol,
		const FlagType	orthogonalize,
		DataType *	alpha,
		DataType *	beta
	)

Tri-diagonalizes matrix A to T using the start vector v. is the Lanczos degree, which will be the size of square matrix T.

The output of this function is not an explicit matrix T, rather are the two arrays alpha of length m and beta of length m+1. The array alpha[:] represents the diagonal elements and beta[1:] represents the off-diagonal elements of the tri-diagonal (m,m) symmetric and positive-definite matrix T.

Lanczos tridiagonalization vs Golub-Kahn bidiagonalization

The Lanczos tri-diagonalization is twice faster (in runtime), as it has only one matrix-vector multiplication. Whereas the Golub-Kahn bi-diagonalization has two matrix-vector multiplications.
The Lanczos tri-diagonalization can only be applied to symmetric matrices. Whereas the Golub-Kahn bi-diagonalization can be applied to any matrix.

Algorithm

The algorithm and notations are obtained from [DEMMEL], p. 57, Algorithm 4.6 (see also [SAAD] p. 137, Algorithm 6.5). However there are four ways to implement the iteration. [PAIGE]_ has shown that the iteration that is implemented below is the most stable against loosing orthogonality of the eigenvectors. For details, see [CULLUM]_ p. 46, and p.48, particularly the algorithm denoted by A(2,7). The differences of these implementations are the order in which \( \alpha_j \) and \( \beta_j \) are defined and the order in which vectors are subtracted from r .

References

[DEMMEL] Demmel, J., Templates for solution of Algebraic Eigenvalue Problems, p. 57.
[SAAD] Saad, Numerical Methods for Large Eigenvalue Problems, p. 137.
[PAIGE] Paige (1980) Accuracy and effectiveness of the Lanczos algorithm for the symmetric eigenproblem.
[CULLUM] Cullum; Willoughby. Lanczos Algorithms for Large Symmetric Eigenvalue Computations. 1. pp.46-48.

Parameters

[in]	A	A linear operator that represents a matrix of size (n,n) and can perform matrix-vector operation with `dot()` method. This matrix should be positive-definite.
[in]	v	Start vector for the Lanczos tri-diagonalization. Column vector of size c n. It could be generated randomly. Often it is generated by the Rademacher distribution with entries c +1 and `-1`.
[in]	n	Size of the square matrix `A`, which is also the size of the vector `v`.
[in]	m	Lanczos degree, which is the number of Lanczos iterations.
[in]	lanczos_tol	The tolerance of the residual error of the Lanczos iteration.
[in]	orthogonalize	Indicates whether to orthogonalize the orthogonal eigenvectors during Lanczos recursive iterations. If set to `0`, no orthogonalization is performed. If set to a negative integer, a newly computed eigenvector is orthogonalized against all the previous eigenvectors (full reorthogonalization). If set to a positive integer, say `q` less than `lanczos_degree`, the newly computed eigenvector is orthogonalized against the last `q` previous eigenvectors (partial reorthogonalization). If set to an integer larger than `lanczos_degree`, it is cut to `lanczos_degree`, which effectively orthogonalizes against all previous eigenvectors (full reorthogonalization).
[out]	alpha	This is a 1D array of size `m`. The array `alpha`[:] constitute the diagonal elements of the tri-diagonal matrix `T`. This is the output and written in place.
[out]	beta	This is a 1D array of size `m`. The array `beta`[:] constitute the off-diagonals of the tri-diagonal matrix `T`. This array is the output and written in place.

Returns: Counter for the Lanczos iterations. Normally, the size of the output matrix should be (m,m), which is the Lanczos degree. However, if the algorithm terminates early, the size of alpha and beta, and hence the output tri-diagonal matrix, is smaller. This counter keeps track of the non-zero size of alpha and beta.

Definition at line 117 of file c_lanczos_tridiagonalization.cpp.

 {
     // buffer_size is number of last orthogonal vectors to keep in the buffer V
     IndexType buffer_size;
     if (orthogonalize == 0 || orthogonalize == 1)
     {
         // At least two vectors must be stored in buffer for Lanczos recursion
         buffer_size = 2;
     }
     else if ((orthogonalize < 0) ||
              (orthogonalize > static_cast<FlagType>(m)))
     {
         // Using full reorthogonalization, keep all of the m vectors in buffer
         buffer_size = m;
     }
     else
     {
         // Orthogonalize with less than m vectors (0 < orthogonalize < m)
         buffer_size = orthogonalize;
     }
  
     // Allocate 2D array (as 1D array, and coalesced row-wise) to store
     // the last buffer_size of orthogonalized vectors of length n. New vectors
     // are stored by cycling through the buffer to replace with old ones.
     DataType* V = new DataType[n * buffer_size];
  
     // Allocate vector r
     DataType* r = new DataType[n];
  
     // Copy v into r
     cVectorOperations<DataType>::copy_vector(v, n, r);
  
     // Initial beta
     DataType initial_beta = cVectorOperations<DataType>::euclidean_norm(r, n);
  
     // Declare iterators
     IndexType j;
     IndexType lanczos_size = 0;
     IndexType num_ortho;
  
     // In the following, beta[j] means beta[j-1] in the Demmel text
     for (j=0; j < m; ++j)
     {
         // Update the size of Lanczos tridiagonal matrix
         ++lanczos_size;
  
         // Normalize r and copy to the j-th column of V
         if (j == 0)
         {
             cVectorOperations<DataType>::copy_scaled_vector(
                     r, n, 1.0/initial_beta, &V[(j % buffer_size)*n]);
         }
         else
         {
             cVectorOperations<DataType>::copy_scaled_vector(
                     r, n, 1.0/beta[j-1], &V[(j % buffer_size)*n]);
         }
  
         // Multiply A to the j-th column of V, write into r
         A->dot(&V[(j % buffer_size)*n], r);
  
         // alpha[j] is V[:, j] dot r
         alpha[j] = cVectorOperations<DataType>::inner_product(
                 &V[(j % buffer_size)*n], r, n);
  
         // Subtract V[:,j] * alpha[j] from r
         cVectorOperations<DataType>::subtract_scaled_vector(
                 &V[(j % buffer_size)*n], n, alpha[j], r);
  
         // Subtract V[:,j-1] * beta[j] from r
         if (j > 0)
         {
             cVectorOperations<DataType>::subtract_scaled_vector(
                     &V[((j-1) % buffer_size)*n], n, beta[j-1], r);
         }
  
         // Gram-Schmidt process (full re-orthogonalization)
         if (orthogonalize != 0)
         {
             // Find how many column vectors are filled so far in the buffer V
             if (j < buffer_size)
             {
                 num_ortho = j+1;
             }
             else
             {
                 num_ortho = buffer_size;
             }
  
             // Gram-Schmidt process
             cOrthogonalization<DataType>::gram_schmidt_process(
                     &V[0], n, buffer_size, j%buffer_size, num_ortho, r);
         }
  
         // beta is norm of r
         beta[j] = cVectorOperations<DataType>::euclidean_norm(r, n);
  
         // Exit criterion when the vector r is zero. If each component of a
         // zero vector has the tolerance epsilon, (which is called lanczos_tol
         // here), the tolerance of norm of r is epsilon times sqrt of n.
         if (beta[j] < lanczos_tol * sqrt(n))
         {
             break;
         }
     }
  
     // Free dynamic memory
     delete[] V;
     delete[] r;
  
     return lanczos_size;
 }

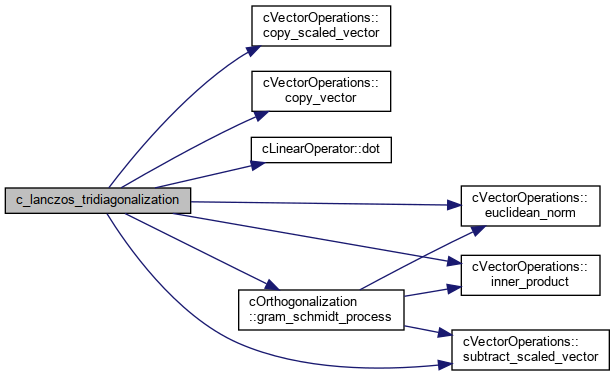
References cVectorOperations< DataType >::copy_scaled_vector(), cVectorOperations< DataType >::copy_vector(), cLinearOperator< DataType >::dot(), cVectorOperations< DataType >::euclidean_norm(), cOrthogonalization< DataType >::gram_schmidt_process(), cVectorOperations< DataType >::inner_product(), and cVectorOperations< DataType >::subtract_scaled_vector().

Referenced by cTraceEstimator< DataType >::_c_stochastic_lanczos_quadrature().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ c_lanczos_tridiagonalization< double >()

template IndexType c_lanczos_tridiagonalization< double >	(	cLinearOperator< double > *	A,
		const double *	v,
		const LongIndexType	n,
		const IndexType	m,
		const double	lanczos_tol,
		const FlagType	orthogonalize,
		double *	alpha,
		double *	beta
	)

◆ c_lanczos_tridiagonalization< float >()

template IndexType c_lanczos_tridiagonalization< float >	(	cLinearOperator< float > *	A,
		const float *	v,
		const LongIndexType	n,
		const IndexType	m,
		const float	lanczos_tol,
		const FlagType	orthogonalize,
		float *	alpha,
		float *	beta
	)

◆ c_lanczos_tridiagonalization< long double >()

template IndexType c_lanczos_tridiagonalization< long double >	(	cLinearOperator< long double > *	A,
		const long double *	v,
		const LongIndexType	n,
		const IndexType	m,
		const long double	lanczos_tol,
		const FlagType	orthogonalize,
		long double *	alpha,
		long double *	beta
	)

Functions