glearn.kernels.RationalQuadratic

class glearn.kernels.RationalQuadratic

Rational quadratic kernel.

The kernel object is used as input argument to the instants of glearn.Covariance class.

Note

For the methods of this class, see the base class glearn.kernels.Kernel.

Parameters:

alphafloat, default=2.0

The parameter \(\alpha\) of the rational quadratic function (see Notes below).

See also

glearn.Covariance

Notes

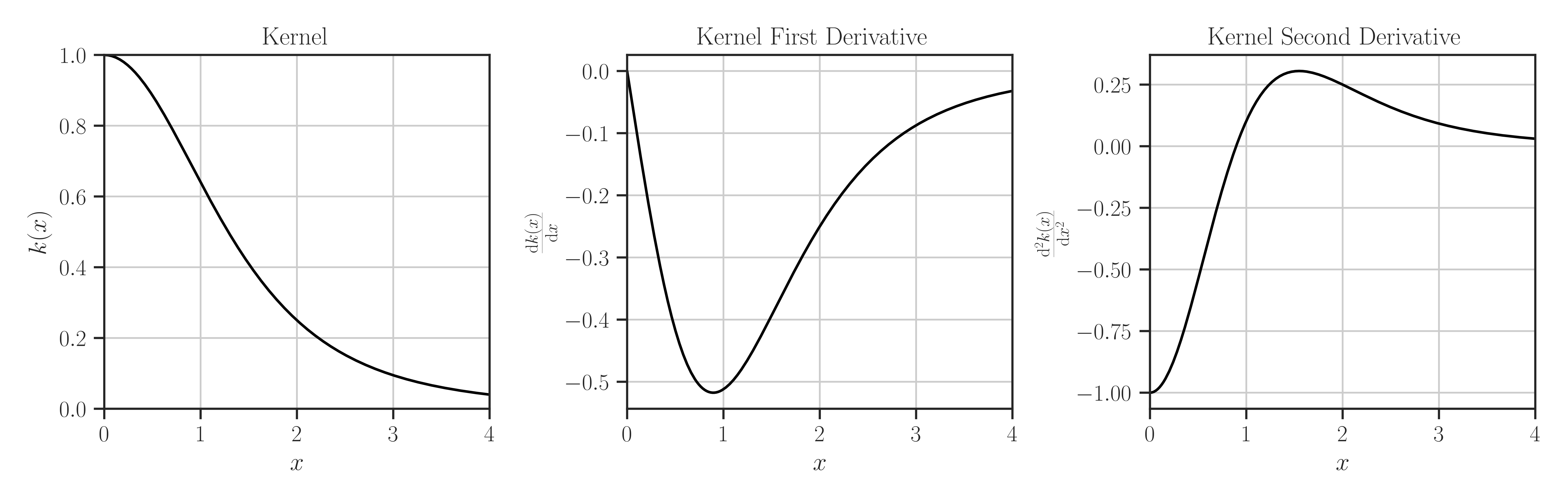
The exponential kernel is defined as

\[k(x) = \left( 1 + \frac{x^2}{2 \alpha} \right)^{-\alpha}.\]

The first derivative of the kernel is

\[\frac{\mathrm{d} k(x)}{\mathrm{d}x} = -x k(x)^{-1-\alpha},\]

and its second derivative is

\[\frac{\mathrm{d} k(x)}{\mathrm{d}x} = x^2 (1 + \alpha^{-1}) k(x)^{-2-\alpha} - k(x)^{-1-\alpha}.\]

Examples

Create Kernel Object:

>>> from glearn import kernels

>>> # Create an exponential kernel
>>> kernel = kernels.RationalQuadratic(alpha=2.0)

>>> # Evaluate kernel at the point x=0.5
>>> x = 0.5
>>> kernel(x)
0.8858131487889274

>>> # Evaluate first derivative of kernel at the point x=0.5
>>> kernel(x, derivative=1)
0.416853246488907

>>> # Evaluate second derivative of kernel at the point x=0.5
>>> kernel(x, derivative=2)
0.416853246488907

>>> # Plot kernel and its first and second derivative
>>> kernel.plot()

Where to Use Kernel Object:

Use the kernel object to define a covariance object:

>>> # Generate a set of sample points
>>> from glearn.sample_data import generate_points
>>> points = generate_points(num_points=50)

>>> # Create covariance object of the points with the above kernel
>>> from glearn import covariance
>>> cov = glearn.Covariance(points, kernel=kernel)