glearn.priors.Uniform#

class glearn.priors.Uniform(a=0, b=inf)#

Uniform distribution.

Note

For the methods of this class, see the base class glearn.priors.Prior.

Parameters:

afloat or array_like[float], default=0: The left point of an interval \([a, b]\) of the uniform distribution. If a is given as an array \((a_1, \dots, a_p)\), the prior is assumed to be \(p\) independent distributions, each on the interval \([a_i, b_i]\).
bfloat or array_like[float], default=numpy.inf: The right point of an interval \([a, b]\) of the uniform distribution. If b is given as an array \((b_1, \dots, b_p)\), the prior is assumed to be \(p\) independent distributions, each on the interval \([a_i, b_i]\).

See also

glearn.priors.Prior

Notes

Single Hyperparameter:

The uniform distribution in the interval \([a, b]\) is defined by the probability density function

\[\begin{split}p(\theta) = \begin{cases} 1, & a \leq \theta \leq b, \\ 0, & \text{otherwise}. \end{cases}\end{split}\]

Multiple Hyperparameters:

If an array of the hyperparameters are given, namely \(\boldsymbol{\theta} = (\theta_1, \dots, \theta_p)\), then the prior is the product of independent priors

\[p(\boldsymbol{\theta}) = p(\theta_1) \dots p(\theta_p).\]

In this case, if the input arguments a and b are given as the arrays \(\boldsymbol{a} = (a_1, \dots, a_p)\) and \(\boldsymbol{b} = (b_1, \dots, b_p)\), each prior \(p(\theta_i)\) is defined as the uniform distribution on the interval \([a_i, b_i]\). In contrary, if a and b are given as the scalars \(a\) and \(b\), then all priors \(p(\theta_i)\) are defined as uniform distributions in the interval \([a, b]\).

Examples

Create Prior Objects:

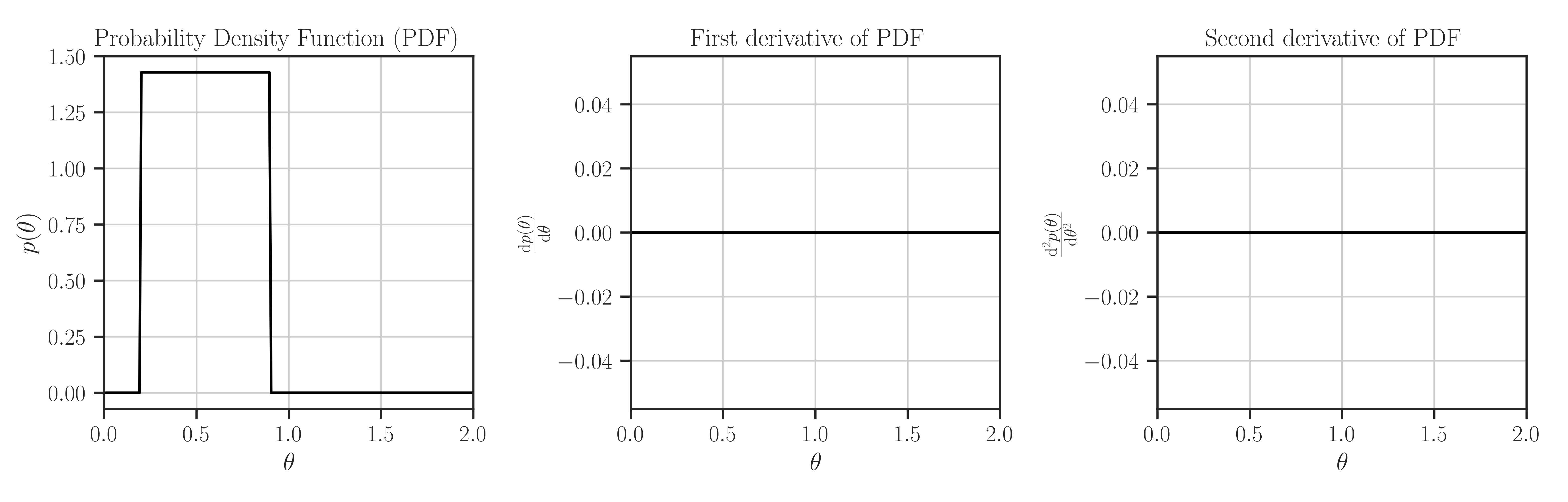
Create uniform prior in the interval \([0.2, 0.9]\):

>>> from glearn import priors
>>> prior = priors.Uniform(0.2, 0.9)

>>> # Evaluate PDF function at multiple locations
>>> t = [0, 0.5, 1]
>>> prior.pdf(t)
array([0.        , 1.42857143, 0.        ])

>>> # Evaluate the Jacobian of the PDF
>>> prior.pdf_jacobian(t)
array([0., 0., 0.])

>>> # Evaluate the Hessian of the PDF
>>> prior.pdf_hessian(t)
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

>>> # Evaluate the log-PDF
>>> prior.log_pdf(t)
-inf

>>> # Evaluate the Jacobian of the log-PDF
>>> prior.log_pdf_jacobian(t)
array([nan, nan, nan])

>>> # Evaluate the Hessian of the log-PDF
>>> prior.log_pdf_hessian(t)
array([[nan,  0.,  0.],
       [ 0., nan,  0.],
       [ 0.,  0., nan]])

>>> # Plot the distribution and its first and second derivative
>>> prior.plot()

Where to Use the Prior object:

Define a covariance model (see glearn.Covariance) where its scale parameter is a prior function.

>>> # Generate a set of sample points
>>> from glearn.sample_data import generate_points
>>> points = generate_points(num_points=50)

>>> # Create covariance object of the points with the above kernel
>>> from glearn import covariance
>>> cov = glearn.Covariance(points, kernel=kernel, scale=prior)

Attributes:

afloat or array_like[float], default=0: Input argument a
bfloat or array_like[float], default=0: Input argument b
meanfloat or array_like[float], default=0: Mean of the distribution

Methods

`suggest_hyperparam`([positive])	Find an initial guess for the hyperparameters based on the peaks of the prior distribution.
`pdf`(x)	Probability density function of the prior distribution.
`pdf_jacobian`(x)	Jacobian of the probability density function of the prior distribution.
`pdf_hessian`(x)	Hessian of the probability density function of the prior distribution.