imate.InterpolateSchatten(kind=’eig’)#

class imate.InterpolateSchatten(A, B=None, p=2, options={}, verbose=False, non_zero_ratio=0.9, kind='eig', tol=0.001)

Evaluates Schatten norm (or anti-norm) of an affine matrix function (no interpolation).

See also

This page describes only the eig method. For other kinds, see imate.InterpolateSchatten().

Note

This class does not interpolate. Rather, it only returns the exact function value, which could be used as a benchmark to test the other interpolation methods.

Parameters:

Anumpy.ndarray, scipy.sparse matrix

A square matrix. Matrix can be dense or sparse.

BNone

In this method, B should always be None, indicating the matrix B is the identity matrix.

pfloat, default=2

The order \(p\) in the Schatten \(p\)-norm which can be real positive, negative or zero.

optionsdict, default={}

At each interpolation point \(t_i\), the value of the Schatten norm is computed using imate.schatten() function which itself calls either of

imate.logdet() (if \(p=0\))
imate.trace() (if \(p>0\))
imate.traceinv() (if \(p < 0\)).

To pass extra parameters to the above functions, pass a dictionary of function arguments to options.

verbosebool, default=False

If True, it prints some information about the computation process.

non_zero_ratiofloat, default=0.9

The ratio of the number of eigenvalues to be assumed non-zero over all eigenvalues. This option is only used for sparse matrices where not all its eigenvalues can be computed, rather, it is assumed some of the eigenvalues are very small and ignored.

tolfloat, default=1e-3

Tolerance of computing eigenvalues. This option is only used for sparse matrices.

Raises:

ValueError: If B is not None.

See also

imate.InterpolateTrace
imate.InterpolateLogdet
imate.schatten

Notes

Schatten Norm:

In this class, the Schatten \(p\)-norm of the matrix \(\mathbf{A}\) is defined by

(1)#\[\begin{split}\Vert \mathbf{A} \Vert_p = \begin{cases} \left| \mathrm{det}(\mathbf{A}) \right|^{\frac{1}{n}}, & p=0, \\ \left| \frac{1}{n} \mathrm{trace}(\mathbf{A}^{p}) \right|^{\frac{1}{p}}, & p \neq 0, \end{cases}\end{split}\]

where \(n\) is the size of the matrix. When \(p \geq 0\), the above definition is the Schatten norm, and when \(p < 0\), the above is the Schatten anti-norm.

Note

Conventionally, the Schatten norm is defined without the normalizing factor \(\frac{1}{n}\) in (1). However, this factor is justified by the continuity granted by

(2)#\[\lim_{p \to 0} \Vert \mathbf{A} \Vert_p = \Vert \mathbf{A} \Vert_0.\]

See [1] (Section 2) and the examples in imate.schatten() for details.

Affine Matrix Function:

This class evaluates the one-parameter matrix function:

\[\tau_p: t \mapsto \| \mathbf{A} + t \mathbf{I} \|_p,\]

where \(t\) is a real parameter and \(\mathbf{I}\) is the identity matrix.

Method of Evaluation:

This class uses the eigenvalues, \(\lambda_i\), of the matrix \(\mathbf{A}\) to compute \(\tau_p(t)\) as follows:

\[\begin{split}\tau_p(t) = \begin{cases} \left( \prod_{i=1}^n (\lambda_i + t) \right)^{\frac{1}{n}}, & p=0, \\ \left( \frac{1}{n} \sum_{i=1}^n (\lambda_i + t)^p \right)^{\frac{1}{p}}, & p \neq 0. \end{cases}\end{split}\]

References

[1]

Ameli, S., and Shadden. S. C. (2022). Interpolating Log-Determinant and Trace of the Powers of Matrix \(\mathbf{A} + t \mathbf{B}\). Statistics and Computing 32, 108. https://doi.org/10.1007/s11222-022-10173-4.

Examples

Basic Usage:

Evaluate the Schatten 2-norm of the affine matrix function \(\mathbf{A} + t \mathbf{I}\):

>>> # Generate two sample matrices (symmetric and positive-definite)
>>> from imate.sample_matrices import correlation_matrix
>>> A = correlation_matrix(size=20, scale=1e-1)

>>> # Initialize interpolator object
>>> from imate import InterpolateSchatten
>>> f = InterpolateSchatten(A, p=2, kind='eig')

>>> # Evaluate at inquiry point t = 0.4
>>> t = 4e-1
>>> f(t)
1.7175340160001518

Alternatively, call imate.InterpolateSchatten.eval() to evaluate at points t:

>>> # This is the same as f(t)
>>> f.eval(t)
1.7175340160001518

Passing Options:

The above examples, the internal computation is passed to imate.trace() function since \(p=2\) is positive. You can pass arguments to the latter function using options argument. To do so, create a dictionary with the keys as the name of the argument. For instance, to use imate.trace(method=’slq’) method with min_num_samples=20 and max_num_samples=100, create the following dictionary:

>>> # Specify arguments as a dictionary
>>> options = {
...     'method': 'slq',
...     'min_num_samples': 20,
...     'max_num_samples': 100
... }

>>> # Pass the options to the interpolator
>>> f = InterpolateSchatten(A, B, options=options, kind='eig')
>>> f(t)
1.7175340160001518

Evaluate on Range of Points:

Evaluate an array of inquiry points t_array:

>>> # Initialize interpolator object
>>> from imate import InterpolateSchatten
>>> f = InterpolateSchatten(A, B, kind='eig')

>>> # Interpolate at an array of points
>>> import numpy
>>> t_array = numpy.logspace(-2, 1, 1000)
>>> norm_array = f(t_array)

Plotting:

To plot the function, call imate.InterpolateSchatten.plot() method. To compare with the true function values, pass compare=True argument.

>>> f.plot(t_array, compare=True)

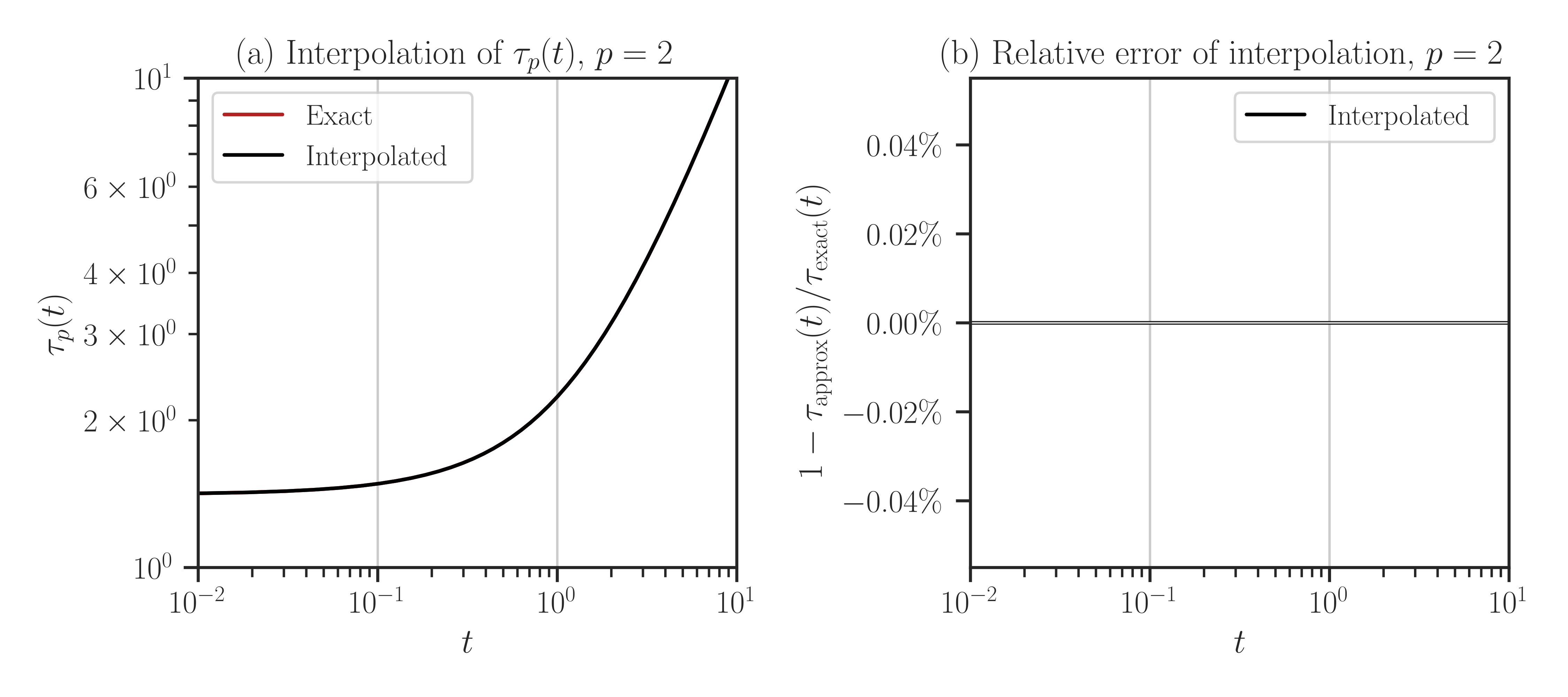
../_images/interpolate_schatten_ext_eig.png

Since the eig method exactly evaluates the function (without interpolation), the error of the result is zero, as shown on the right-hand side plot.

Attributes:

kindstr: Method of interpolation. For this class, kind is ext.
verbosebool: Verbosity of the computation process
nint: Size of the matrix
qint: Number of interpolant points. For this class, q is zero.
pfloat: Order of Schatten \(p\)-norm

Methods

__call__	See `imate.InterpolateSchatten.__call__()`.
eval	See `imate.InterpolateSchatten.eval()`.
interpolate	See `imate.InterpolateSchatten.interpolate()`.
bound	See `imate.InterpolateSchatten.bound()`.
upper_bound	See `imate.InterpolateSchatten.upper_bound()`.
plot	See `imate.InterpolateSchatten.plot()`.