imate.InterpolateSchatten.plot#

InterpolateSchatten.plot(t, normalize=True, compare=False)#

Plot the interpolation results.

Parameters:
tnumpy.array

Inquiry points to be interpolated.

normalizebool, default: False

If set to False the function \(\tau_p = \Vert \mathbf{A} + t \mathbf{B} \Vert_p\) is plotted. If set to True, it plots the normalized function

\[\tau_p(t) = \frac{\Vert \mathbf{A} + t \mathbf{B} \Vert_{p}}{\Vert \mathbf{B} \Vert_p}.\]
comparebool, default=False

If True, it computes the exact function values (without interpolation), then compares it with the interpolated solution to estimate the relative error of interpolation.

Note

When this option is enabled, the exact solution will be computed for all inquiry points, which can take a very long time.

Raises:
ImportError

If matplotlib is not installed.

ValueError

If t is not an array of size greater than one.

Notes

Plotted Function:

  • When kind is either of ext, eig, mbf, imbf, rpf, or rbf, the function \(\tau_p(t)\) is plotted, which is defined as follows. If normalize is False, then

    \[\tau_p(t) = \Vert \mathbf{A} + t \mathbf{B} \Vert_p.\]

    If normalize is True, then

    \[\frac{\Vert \mathbf{A} + t \mathbf{B} \Vert_{p}}{ \Vert \mathbf{B} \Vert_p}.\]

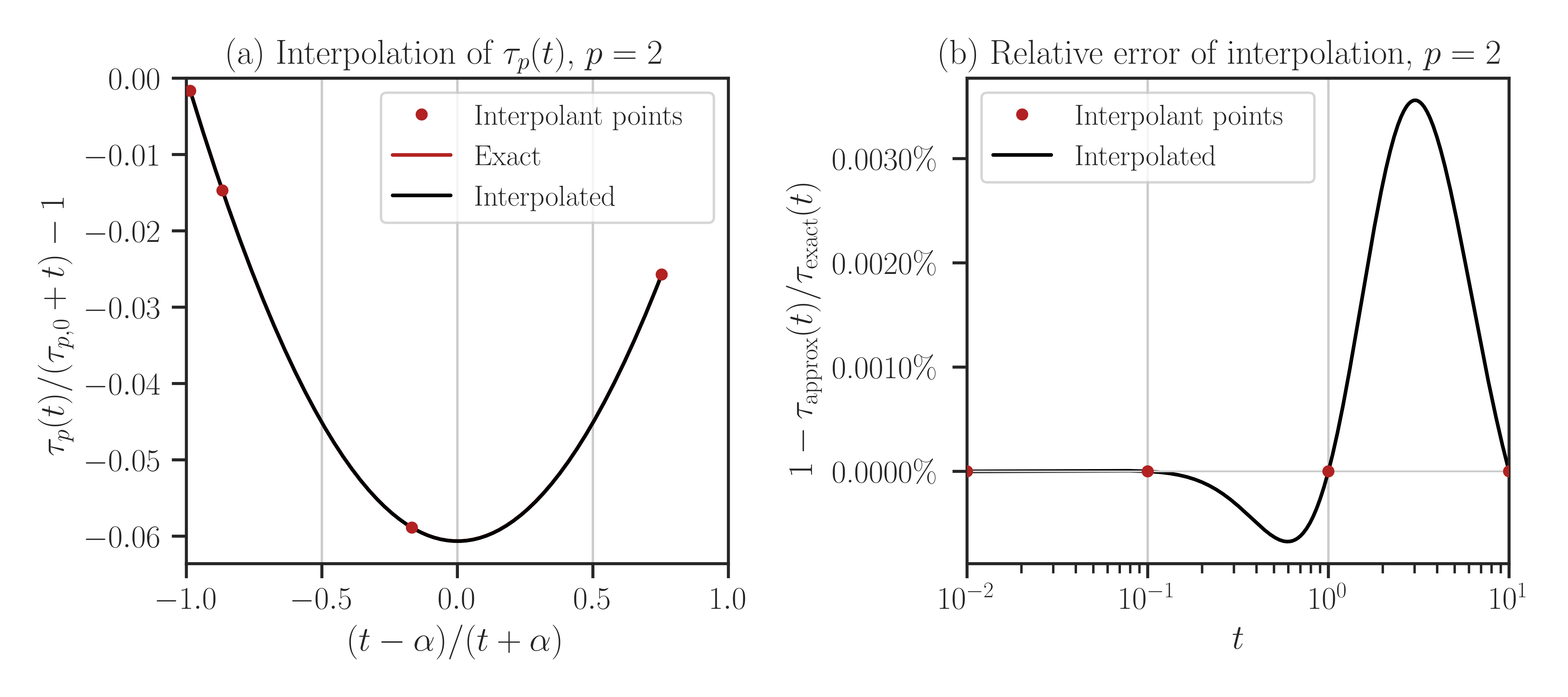
  • On the other hand, if kind=crf or kind=spl, the function \(y_p(x)\) is plotted, which is defined as follows:

    \[x = \frac{t - \alpha}{t + \alpha},\]

    where \(\alpha\) is the scale parameter in imate.InterpolateSchatten(kind=’crf’) for kind=crf. If kind=spl, then \(\alpha=1\). Also

    \[y_p = \frac{\tau_p(t)}{\tau_p(0) + t} - 1.\]

Graphical Backend:

  • If no graphical backend exists (such as running the code on a remote server or manually disabling the X11 backend), the plot will not be shown, rather, it will ve saved as an svg file in the current directory.

  • If the executable latex is on the path, the plot is rendered using \(\rm\LaTeX\), which then, it takes a bit longer to produce the plot.

  • If \(\rm\LaTeX\) is not installed, it uses any available San-Serif font to render the plot.

To manually disable interactive plot display, and save the plot as SVG instead, add the following in the very beginning of your code before importing imate:

>>> import os
>>> os.environ['IMATE_NO_DISPLAY'] = 'True'

Examples

Create an interpolator object \(f\) using four interpolant points \(t_i\):

>>> # Generate sample matrices (symmetric positive-definite)
>>> from imate.sample_matrices import correlation_matrix
>>> A = correlation_matrix(size=20, scale=1e-1)
>>> B = correlation_matrix(size=20, scale=2e-2)

>>> # Initialize interpolator object
>>> from imate import InterpolateSchatten
>>> ti = [1e-2, 1e-1, 1, 1e1]
>>> f = InterpolateSchatten(A, B, ti=ti)

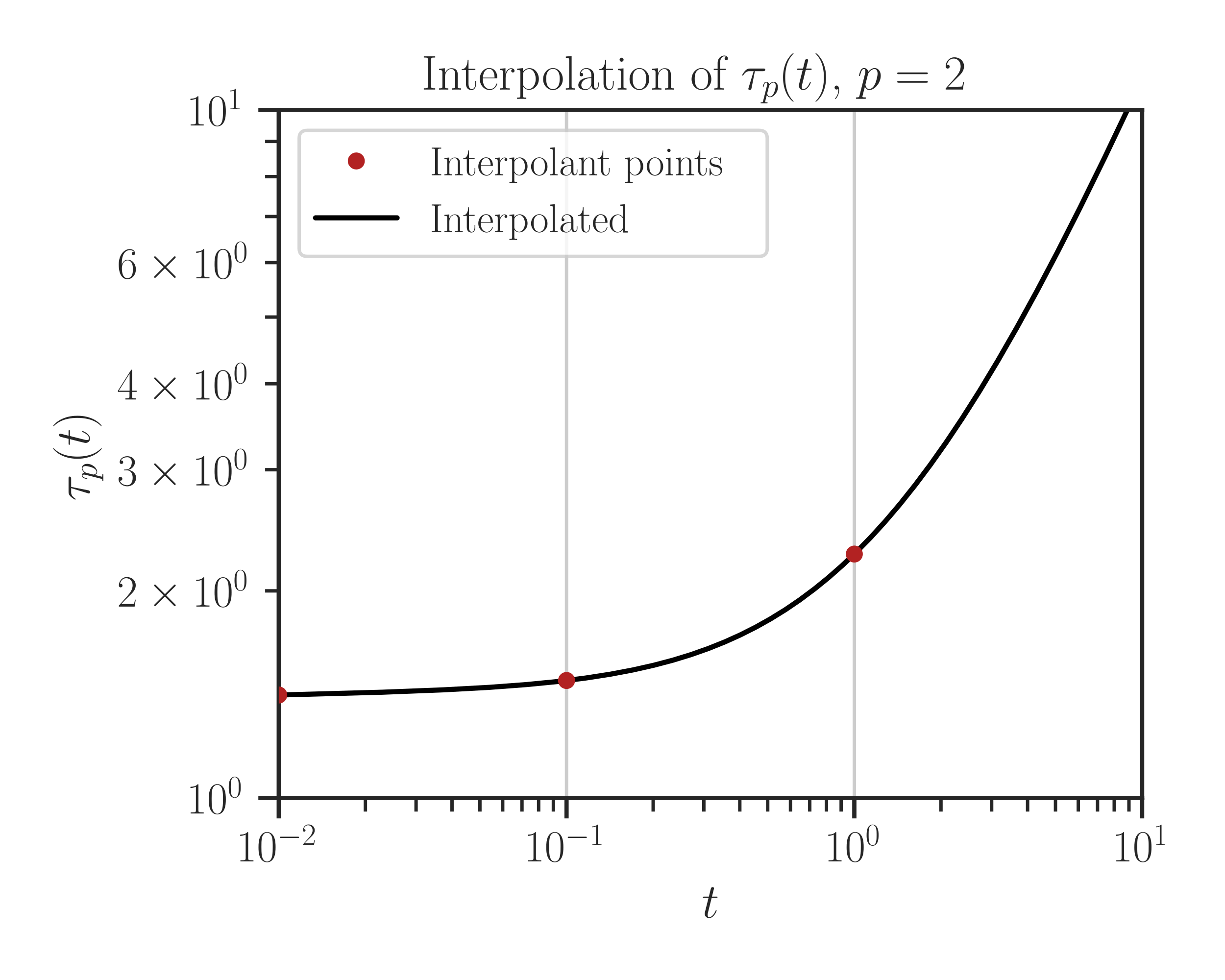
Define an array if inquiry point t and call imate.InterpolateSchatten.plot() function to plot the interpolation of the function \(f(t)\):

>>> import numpy
>>> t_array = numpy.logspace(-2, 1, 1000)
>>> f.plot(t_array)
../_images/interpolate_schatten_2.png

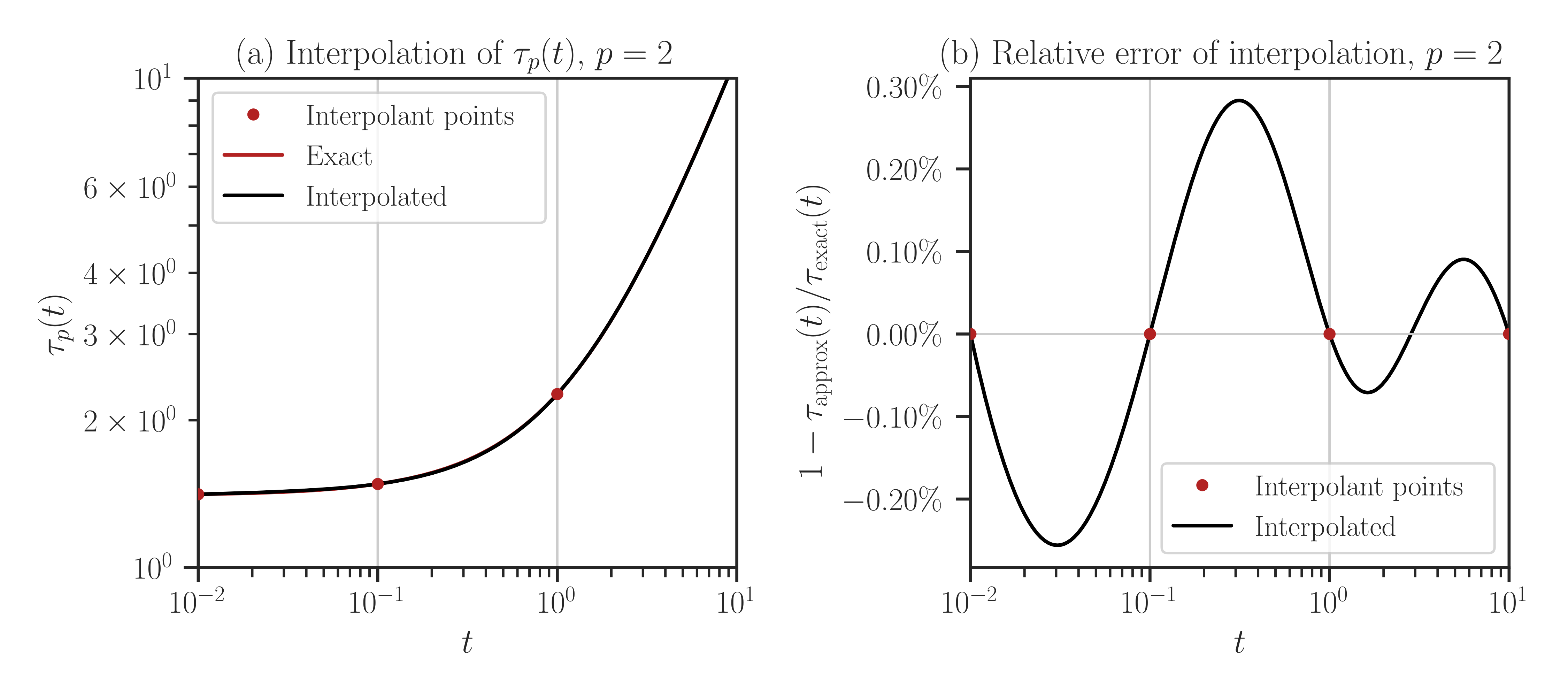
To compare with the true values (without interpolation), pass compare=True to the above function.

Warning

By setting compare to True, every point in the array t is evaluated both using interpolation and with the exact method (no interpolation). If the size of t is large, this may take a very long run time.

>>> f.plot(t_array, normalize=True, compare=True)
../_images/interpolate_schatten_3.png

Plotting for Chebyshev and Spline Methods:

As mentioned in the Notes in the above, if kind=crf or kind=spl, the transformed function \(y_p(x)\) is plotted as shown in the example below:

>>> # Recreate interpolating object, but using crf method
>>> f = InterpolateSchatten(A, B, kind='crf', ti=ti)
>>> t_array = numpy.logspace(-2, 1, 1000)
>>> f.plot(t_array)
../_images/interpolate_schatten_4.png