imate.InterpolateSchatten(kind=’imbf’)#

class imate.InterpolateSchatten(A, B=None, p=2, options={}, verbose=False, ti=[], kind='imbf', basis_func_type='ortho2')

Interpolate Schatten norm (or anti-norm) of an affine matrix function using inverse monomial basis functions (IMBF) method.

See also

This page describes only the imbf method. For other kinds, see imate.InterpolateSchatten().

Parameters:

Anumpy.ndarray, scipy.sparse matrix

Symmetric positive-definite matrix (positive-definite if p is non-positive). Matrix can be dense or sparse.

Warning

Symmetry and positive (semi-) definiteness of A will not be checked. Make sure A satisfies these conditions.

Bnumpy.ndarray, scipy.sparse matrix, default=None

Symmetric positive-definite matrix (positive-definite if p is non-positive). Matrix can be dense or sparse. B should have the same size and type of A. If B is None (default value), it is assumed that B is the identity matrix.

Warning

Symmetry and positive (semi-) definiteness of B will not be checked. Make sure B satisfies these conditions.

pfloat, default=2

The order \(p\) in the Schatten \(p\)-norm which can be real positive, negative or zero.

optionsdict, default={}

At each interpolation point \(t_i\), the Schatten norm is computed using imate.schatten() function which itself calls either of

imate.logdet() (if \(p=0\))
imate.trace() (if \(p>0\))
imate.traceinv() (if \(p < 0\)).

The options passes a dictionary of arguments to the above functions.

verbosebool, default=False

If True, it prints some information about the computation process.

tifloat or array_like(float), default=None

Interpolation points, which can be a single number, a list or an array of interpolation points. The interpolator honors the exact function values at the interpolant points.

basis_func_type: {‘non-ortho’, ‘ortho’, ‘ortho2’}, default=’ortho2’

Type of basis functions (see Notes below).

See also

imate.InterpolateTrace
imate.InterpolateLogdet
imate.schatten

Notes

Schatten Norm:

In this class, the Schatten \(p\)-norm of the matrix \(\mathbf{A}\) is defined by

(1)#\[\begin{split}\Vert \mathbf{A} \Vert_p = \begin{cases} \left| \mathrm{det}(\mathbf{A}) \right|^{\frac{1}{n}}, & p=0, \\ \left| \frac{1}{n} \mathrm{trace}(\mathbf{A}^{p}) \right|^{\frac{1}{p}}, & p \neq 0, \end{cases}\end{split}\]

where \(n\) is the size of the matrix. When \(p \geq 0\), the above definition is the Schatten norm, and when \(p < 0\), the above is the Schatten anti-norm.

Note

Conventionally, the Schatten norm is defined without the normalizing factor \(\frac{1}{n}\) in (1). However, this factor is justified by the continuity granted by

(2)#\[\lim_{p \to 0} \Vert \mathbf{A} \Vert_p = \Vert \mathbf{A} \Vert_0.\]

See [1] (Section 2) and the examples in imate.schatten() for details.

Interpolation of Affine Matrix Function:

This class interpolates the one-parameter matrix function:

\[t \mapsto \| \mathbf{A} + t \mathbf{B} \|_p,\]

where the matrices \(\mathbf{A}\) and \(\mathbf{B}\) are symmetric and positive semi-definite (positive-definite if \(p < 0\)) and \(t \in [t_{\inf}, \infty)\) is a real parameter where \(t_{\inf}\) is the minimum \(t\) such that \(\mathbf{A} + t_{\inf} \mathbf{B}\) remains positive-definite.

Method of Interpolation:

Define the function

\[\tau_p(t) = \frac{\Vert \mathbf{A} + t \mathbf{B} \Vert_p} {\Vert \mathbf{B} \Vert_p},\]

and \(\tau_{p, 0} = \tau_p(0)\). Then, we approximate \(\tau_p(t)\) by

\[\tau_p(t) \approx \tau_{p, 0} + \sum_{i = 0}^q w_i \phi_i(t),\]

where \(\phi_i\) are some known basis functions, and \(w_i\) are the coefficients of the linear basis functions. The first coefficient is set to \(w_{0} = 1\) and the rest of the weights are to be found from the known function values \(\tau_{p, i} = \tau_p(t_i)\) at the given interpolant points \(t_i\).

Interpolation Points:

The best practice is to provide an array of interpolation points that are equally distanced on the logarithmic scale. For instance, to produce four interpolation points in the interval \([10^{-2}, 1]\):

>>> import numpy
>>> ti = numpy.logspace(-2, 1, 4)

Basis Functions:

In this module, three kinds of basis functions which can be set by the argument basis_func_type.

When basis_func_type is set to non-ortho, the basis functions are the inverse of the monomial functions defined by

\[\phi_i(t) = t^{\frac{1}{i+1}}, \qquad i = 0, \dots, q.\]

Warning

The non-orthogonal basis functions can lead to ill-conditioned system of equations for finding the weight coefficients \(w_i\). When the number of interpolating points is large (such as \(q > 6\)), it is recommended to use the orthogonalized set of basis functions described next.

When basis_func_type is set to 'ortho' or 'ortho2', the orthogonal form of the above basis functions are used. Orthogonal basis functions are formed by the above non-orthogonal functions as

\[\phi_i^{\perp}(t) = \alpha_i \sum_{j=1}^i a_{ij} \phi_j(t)\]

The coefficients \(\alpha_i\) and \(a_{ij}\) can be obtained by the python package ortho. These coefficients are hard-coded in this function up to \(i = 9\). Thus, in this module, up to nine interpolant points are supported.

The difference between ortho and orth2 basis functions is that in the former, the functions \(\phi_i\) for all \(i=0,\dots, q\) are orthogonalized, whereas in the latter, only the functions \(i=1,\dots,q\) (excluding \(i=0\)) are orthogonalized.

Note

The recommended basis function type is 'ortho2'.

How to Generate the Basis Functions:

The coefficients \(\alpha\) and \(a\) of the basis functions are hard-coded up to \(q=9\) in this class. To generate further basis functions, use ortho python package.

Install this package by

pip install ortho

To generate the coefficients corresponding to ortho basis:
```
gen-orth -n 9 -s 0
```
To generate the coefficients corresponding to ortho2 basis:
```
gen-orth -n 9 -s 1
```

References

[1]

Ameli, S., and Shadden. S. C. (2022). Interpolating Log-Determinant and Trace of the Powers of Matrix \(\mathbf{A} + t \mathbf{B}\). Statistics and Computing 32, 108. https://doi.org/10.1007/s11222-022-10173-4.

Examples

Basic Usage:

Interpolate the Schatten 2-norm of the affine matrix function \(\mathbf{A} + t \mathbf{B}\) using imbf algorithm and the interpolating points \(t_i = [10^{-2}, 10^{-1}, 1, 10]\).

>>> # Generate two sample matrices (symmetric and positive-definite)
>>> from imate.sample_matrices import correlation_matrix
>>> A = correlation_matrix(size=20, scale=1e-1)
>>> B = correlation_matrix(size=20, scale=2e-2)

>>> # Initialize interpolator object
>>> from imate import InterpolateSchatten
>>> ti = [1e-2, 1e-1, 1, 1e1]
>>> f = InterpolateSchatten(A, B, p=2, kind='imbf', ti=ti)

>>> # Interpolate at an inquiry point t = 0.4
>>> t = 4e-1
>>> f(t)
1.7328745175033962

Alternatively, call imate.InterpolateSchatten.interpolate() to interpolate at points t:

>>> # This is the same as f(t)
>>> f.interpolate(t)
1.7328745175033962

To evaluate the exact value of the Schatten norm at point t without interpolation, call imate.InterpolateSchatten.eval() function:

>>> # This evaluates the function value at t exactly (no interpolation)
>>> f.eval(t)
1.7374809371539666

It can be seen that the relative error of interpolation compared to the exact solution in the above is \(0.26 \%\) using only four interpolation points \(t_i\), which is a remarkable result.

Warning

Calling imate.InterpolateSchatten.eval() may take a longer time to compute as it computes the function exactly. Particularly, if t is a large array, it may take a very long time to return the exact values.

Passing Options:

The above examples, the internal computation is passed to imate.trace() function since \(p=2\) is positive. You can pass arguments to the latter function using options argument. To do so, create a dictionary with the keys as the name of the argument. For instance, to use imate.trace(method=’slq’) method with min_num_samples=20 and max_num_samples=100, create the following dictionary:

>>> # Specify arguments as a dictionary
>>> options = {
...     'method': 'slq',
...     'min_num_samples': 20,
...     'max_num_samples': 100
... }

>>> # Pass the options to the interpolator
>>> f = InterpolateSchatten(A, B, p=2, options=options, kind='imbf',
...                         ti=ti)
>>> f(t)
1.7397564159794918

You may get a different result than the above as the slq method is a randomized method.

Interpolate on Range of Points:

Once the interpolation object f in the above example is instantiated, calling imate.InterpolateSchatten.interpolate() on a list of inquiry points t has almost no computational cost. The next example inquires interpolation on 1000 points t:

Interpolate an array of inquiry points t_array:

>>> # Create an interpolator object again
>>> ti = 1e-1
>>> f = InterpolateSchatten(A, B, kind='imbf', ti=ti)

>>> # Interpolate at an array of points
>>> import numpy
>>> t_array = numpy.logspace(-2, 1, 1000)
>>> norm_array = f.interpolate(t_array)

Plotting Interpolation and Compare with Exact Solution:

To plot the interpolation results, call imate.InterpolateSchatten.plot() function. To compare with the true values (without interpolation), pass compare=True to the above function.

Warning

By setting compare to True, every point in the array t is evaluated both using interpolation and with the exact method (no interpolation). If the size of t is large, this may take a very long run time.

>>> f.plot(t_array, normalize=True, compare=True)

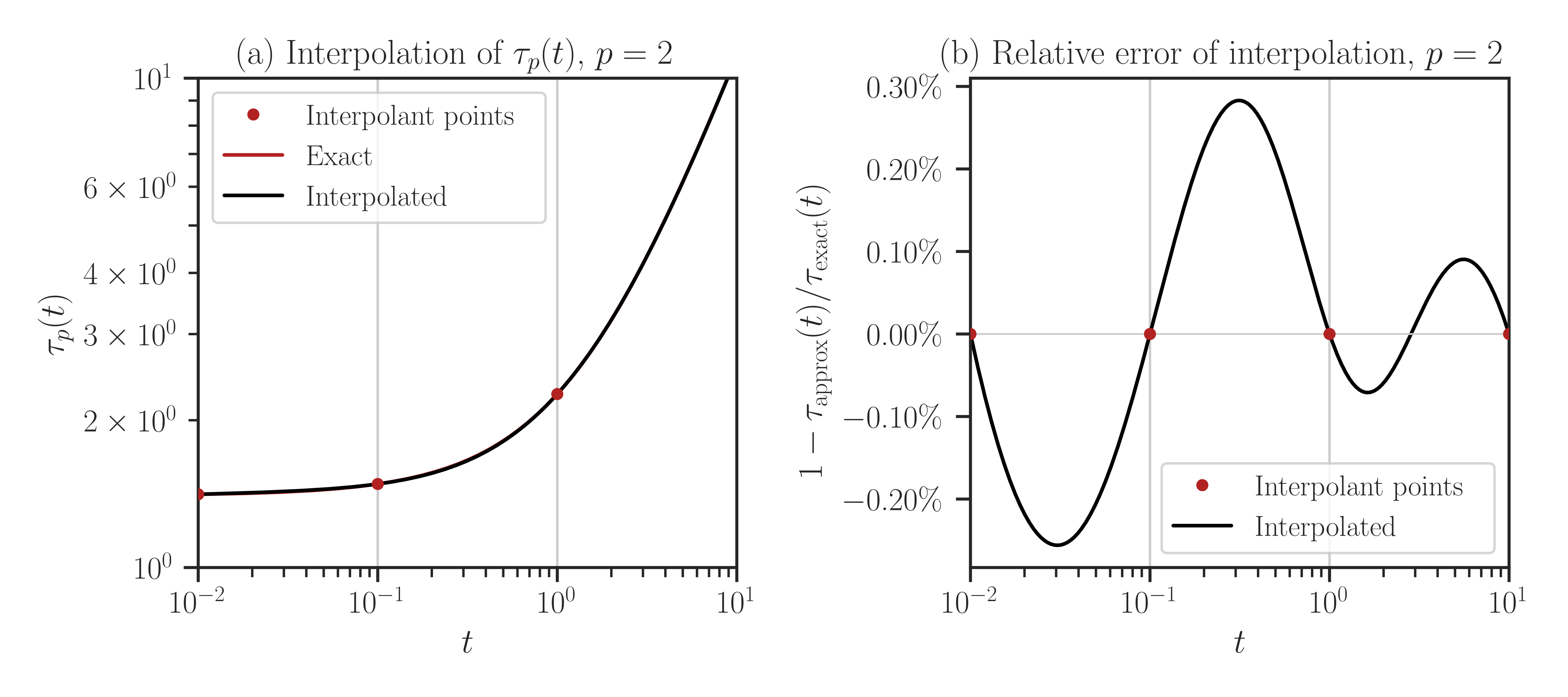
../_images/interpolate_schatten_imbf.png

From the error plot in the above, it can be seen that with only four interpolation points, the error of interpolation for a wide range of \(t\) is no more than \(0.3 \%\). Also, note that the error on the interpolant points \(t_i=[10^{-2}, 10^{-1}, 1, 10]\) is zero since the interpolation scheme honors the exact function value at the interpolation points.

Attributes:

kindstr: Method of interpolation. For this class, kind is imbf.
verbosebool: Verbosity of the computation process
nint: Size of the matrix
qint: Number of interpolant points.
pfloat: Order of Schatten \(p\)-norm

Methods

__call__	See `imate.InterpolateSchatten.__call__()`.
eval	See `imate.InterpolateSchatten.eval()`.
interpolate	See `imate.InterpolateSchatten.interpolate()`.
bound	See `imate.InterpolateSchatten.bound()`.
upper_bound	See `imate.InterpolateSchatten.upper_bound()`.
plot	See `imate.InterpolateSchatten.plot()`.