imate.InterpolateSchatten#

class imate.InterpolateSchatten(A, B=None, p=2, options={}, verbose=False, kind='imbf', ti=[], **kwargs)#

Interpolate Schatten norm (or anti-norm) of an affine matrix function.

Parameters:
Anumpy.ndarray, scipy.sparse matrix

Symmetric positive-definite matrix (positive-definite if p is non-positive). Matrix can be dense or sparse.

Warning

Symmetry and positive (semi-) definiteness of A will not be checked. Make sure A satisfies these conditions.

Bnumpy.ndarray, scipy.sparse matrix, default=None

Symmetric positive-definite matrix (positive-definite if p is non-positive). Matrix can be dense or sparse. B should have the same size and type of A. If B is None (default value), it is assumed that B is the identity matrix.

Warning

Symmetry and positive (semi-) definiteness of B will not be checked. Make sure B satisfies these conditions.

pfloat, default=2

The order \(p\) in the Schatten \(p\)-norm which can be real positive, negative or zero.

optionsdict, default={}

At each interpolation point \(t_i\), the Schatten norm is computed using imate.schatten() function which itself calls either of

The options passes a dictionary of arguments to the above functions.

verbosebool, default=False

If True, it prints some information about the computation process.

kind{‘ext’, ‘eig’, ‘mbf’, ‘imbf’, ‘rbf’, ‘crf’, ‘spl’, ‘rpf’}, default: ‘imbf’

The algorithm of interpolation. See documentation for each specific algorithm:

tifloat or array_like(float), default=None

Interpolation points, which can be a single point, a list, or an array of points. The interpolator honors the exact function values at the interpolant points. If an empty list is given, i.e., [], depending on the algorithm, a default list of interpolant points is used. Also, the size of the array of ti depends on the algorithm as follows. If kind is:

  • ext or eig, the no ti is required.

  • mbf, then a single point ti may be specified.

  • imbf, spl, or rbf, then a list of ti with arbitrary size may be specified.

  • crf or rpf, then a list of ti points with even size may be specified.

kwargs**kwargs

Additional arguments to pass to each specific algorithm. See documentation for each kind in the above.

See also

imate.InterpolateTrace
imate.InterpolateLogdet
imate.schatten

Notes

Schatten Norm:

In this class, the Schatten \(p\)-norm of the matrix \(\mathbf{A}\) is defined by

(1)#\[\begin{split}\Vert \mathbf{A} \Vert_p = \begin{cases} \left| \mathrm{det}(\mathbf{A}) \right|^{\frac{1}{n}}, & p=0, \\ \left| \frac{1}{n} \mathrm{trace}(\mathbf{A}^{p}) \right|^{\frac{1}{p}}, & p \neq 0, \end{cases}\end{split}\]

where \(n\) is the size of the matrix. When \(p \geq 0\), the above definition is the Schatten norm, and when \(p < 0\), the above is the Schatten anti-norm.

Note

Conventionally, the Schatten norm is defined without the normalizing factor \(\frac{1}{n}\) in (1). However, this factor is justified by the continuity granted by

(2)#\[\lim_{p \to 0} \Vert \mathbf{A} \Vert_p = \Vert \mathbf{A} \Vert_0.\]

See [1] (Section 2) and the examples in imate.schatten() for details.

Interpolation of Affine Matrix Function:

This class interpolates the Schatten norm (or anti-norm) of the one-parameter matrix function:

\[\tau_p: t \mapsto \| \mathbf{A} + t \mathbf{B} \|_p,\]

where the matrices \(\mathbf{A}\) and \(\mathbf{B}\) are symmetric and positive semi-definite (positive-definite if \(p < 0\)) and \(t \in [t_{\inf}, \infty)\) is a real parameter where \(t_{\inf}\) is the minimum \(t\) such that \(\mathbf{A} + t_{\inf} \mathbf{B}\) remains positive-definite.

The interpolator is initialized by providing \(q\) interpolant points \(t_i\), \(i = 1, \dots, q\), which are often given in a logarithmically spaced interval \(t_i \in [t_1, t_p]\). The interpolator can interpolate the above function at arbitrary inquiry points \(t \in [t_1, t_p]\) using various methods.

References

[1]

Ameli, S., and Shadden. S. C. (2022). Interpolating Log-Determinant and Trace of the Powers of Matrix \(\mathbf{A} + t \mathbf{B}\). Statistics and Computing 32, 108. https://doi.org/10.1007/s11222-022-10173-4.

Examples

Basic Usage:

Interpolate the Schatten 2-norm of the affine matrix function \(\mathbf{A} + t \mathbf{B}\) using imbf algorithm and the interpolating points \(t_i = [10^{-2}, 10^{-1}, 1, 10]\).

>>> # Generate two sample matrices (symmetric and positive-definite)
>>> from imate.sample_matrices import correlation_matrix
>>> A = correlation_matrix(size=20, scale=1e-1)
>>> B = correlation_matrix(size=20, scale=2e-2)

>>> # Initialize interpolator object
>>> from imate import InterpolateSchatten
>>> ti = [1e-2, 1e-1, 1, 1e1]
>>> f = InterpolateSchatten(A, B, p=2, kind='imbf', ti=ti)

>>> # Interpolate at an inquiry point t = 0.4
>>> t = 4e-1
>>> f(t)
1.7328745175033962

Alternatively, call imate.InterpolateSchatten.interpolate() to interpolate at points t:

>>> # This is the same as f(t)
>>> f.interpolate(t)
1.7328745175033962

To evaluate the exact value of the Schatten norm at point t without interpolation, call imate.InterpolateSchatten.eval() function:

>>> # This evaluates the function value at t exactly (no interpolation)
>>> f.eval(t)
1.7374809371539666

It can be seen that the relative error of interpolation compared to the exact solution in the above is \(0.26 \%\) using only four interpolation points \(t_i\), which is a remarkable result.

Warning

Calling imate.InterpolateSchatten.eval() may take a longer time to compute as it computes the function exactly. Particularly, if t is a large array, it may take a very long time to return the exact values.

Arguments Specific to Algorithms:

In the above example, the imbf algorithm is used. See more arguments of this algorithm at imate.InterpolateSchatten(kind=’imbf’). In the next example, we pass basis_func_type specific to this algorithm:

>>> # Passing kwatgs specific to imbf algorithm
>>> f = InterpolateSchatten(A, B, p=2, kind='imbf', ti=ti,
...                         basis_func_type='ortho2')
>>> f(t)
1.7328745175033962

You may choose other algorithms using kind argument. For instance, the next example uses the Chebyshev rational functions with an additional argument func_type specific to this method. See more details at imate.InterpolateSchatten(kind=’crf’).

>>> # Generate two sample matrices (symmetric and positive-definite)
>>> f = InterpolateSchatten(A, B, p=2, kind='crf', ti=ti,
...                         func_type=1)
>>> f(t)
1.737489512386539

Passing Options:

The above examples, the internal computation is passed to imate.trace() function since \(p=2\) is positive. You can pass arguments to the latter function using options argument. To do so, create a dictionary with the keys as the name of the argument. For instance, to use imate.trace(method=’slq’) method with min_num_samples=20 and max_num_samples=100, create the following dictionary:

>>> # Specify arguments as a dictionary
>>> options = {
...     'method': 'slq',
...     'min_num_samples': 20,
...     'max_num_samples': 100
... }

>>> # Pass the options to the interpolator
>>> f = InterpolateSchatten(A, B, p=2, options=options, kind='imbf',
...                         ti=ti)
>>> f(t)
1.7291144488066212

You may get a different result than the above as the slq method is a randomized method.

Interpolate on Range of Points:

Once the interpolation object f in the above example is instantiated, calling imate.InterpolateSchatten.interpolate() on a list of inquiry points t has almost no computational cost. The next example inquires interpolation on 1000 points t:

Interpolate an array of inquiry points t_array:

>>> # Create an interpolator object again
>>> ti = [1e-2, 1e-1, 1, 1e1]
>>> f = InterpolateSchatten(A, B, ti=ti)

>>> # Interpolate at an array of points
>>> import numpy
>>> t_array = numpy.logspace(-2, 1, 1000)
>>> norm_array = f.interpolate(t_array)

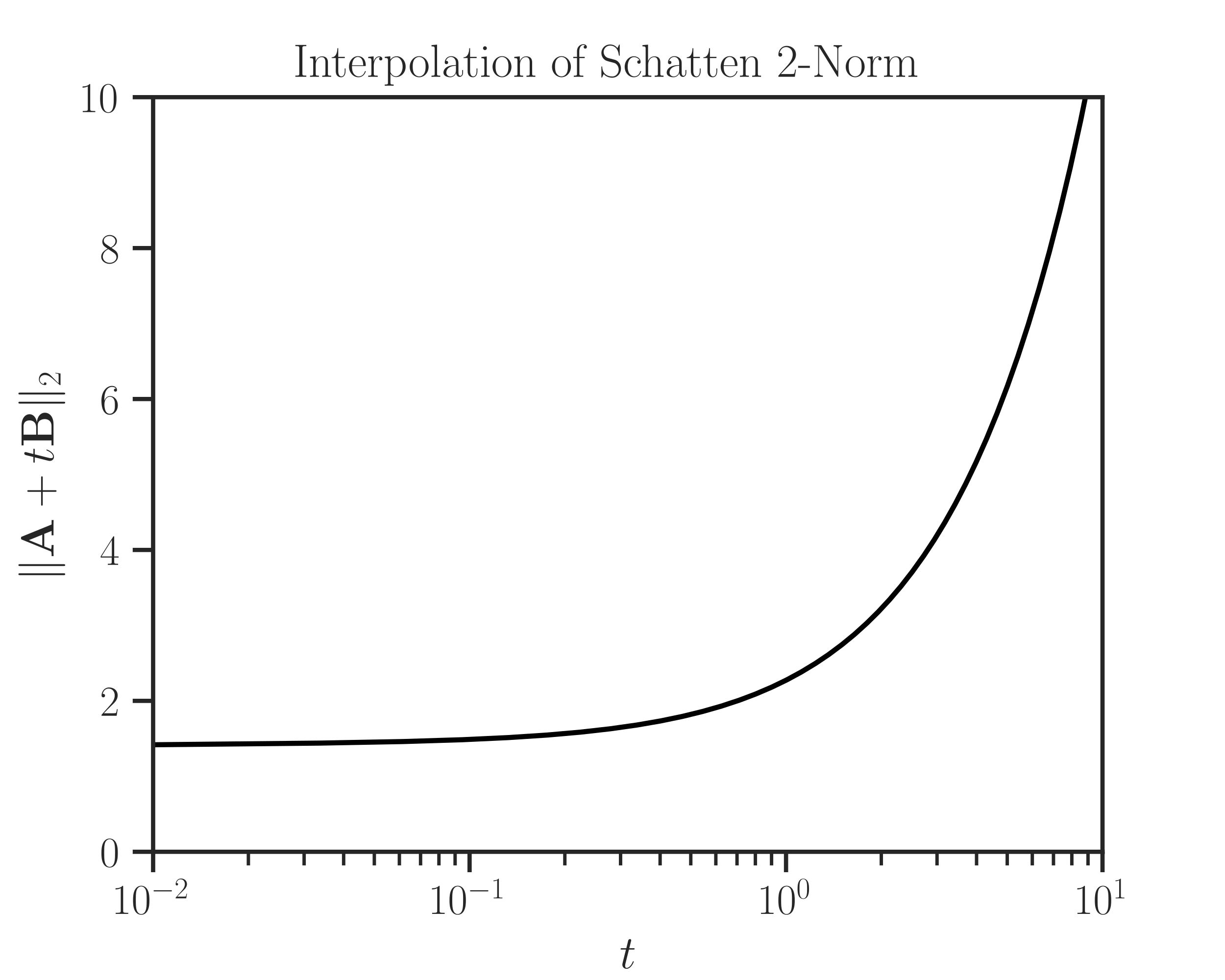
One may plot the above interpolated results as follows:

>>> import matplotlib.pyplot as plt

>>> # Plot settings (optional)
>>> from imate._utilities import set_custom_theme
>>> set_custom_theme(font_scale=1.15)

>>> plt.semilogx(t_array, norm_array, color='black')
>>> plt.xlim([t_array[0], t_array[-1]])
>>> plt.ylim([0, 10])
>>> plt.xlabel('$t$')
>>> plt.ylabel('$\Vert \mathbf{A} + t \mathbf{B} \Vert_{2}$')
>>> plt.title('Interpolation of Schatten 2-Norm')
>>> plt.show()
../_images/interpolate_schatten_1.png

Plotting Interpolation and Compare with Exact Solution:

A more convenient way to plot the interpolation result is to call imate.InterpolateSchatten.plot() function.

>>> f.plot(t_array)
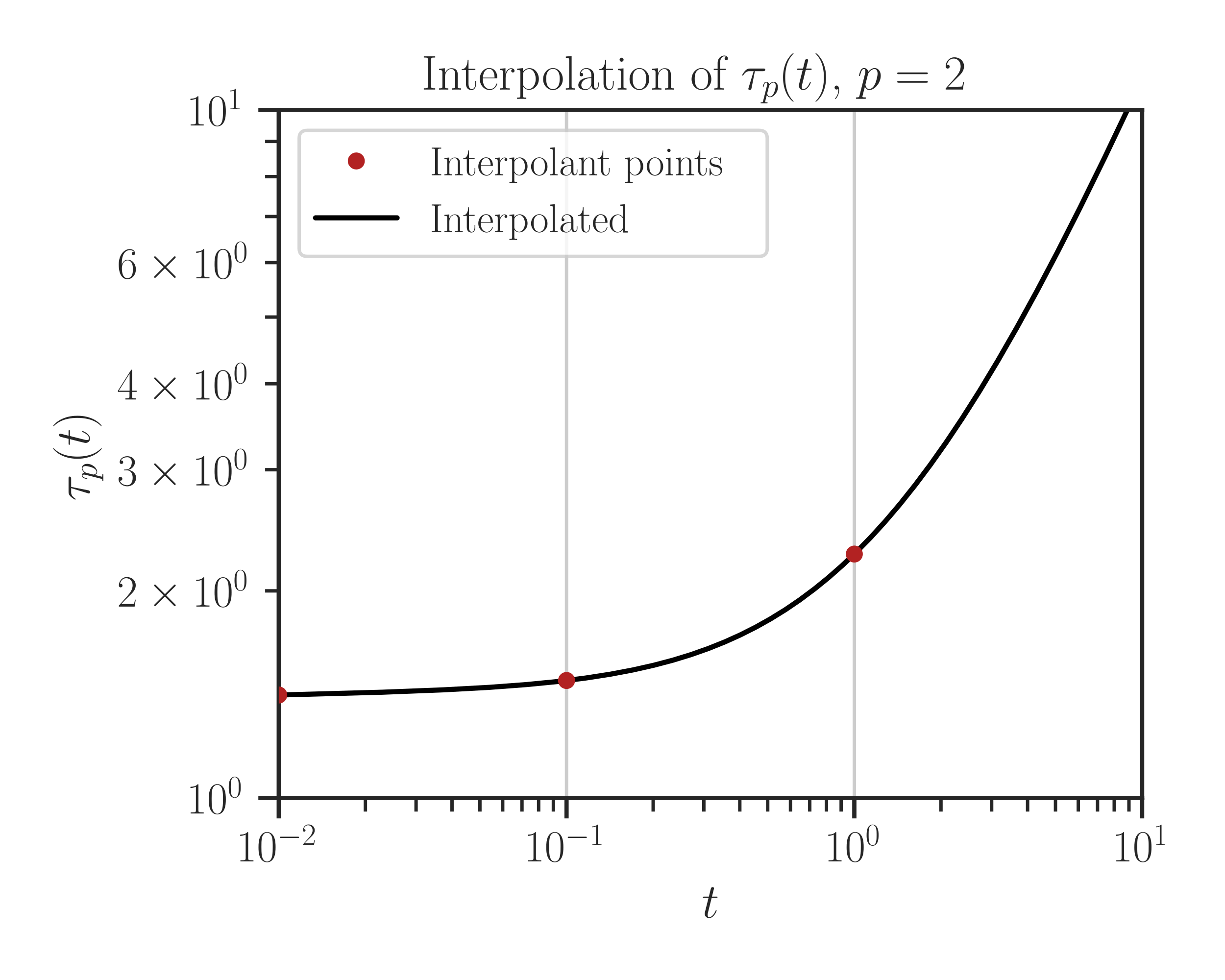
../_images/interpolate_schatten_2.png

In the above, \(\tau_p = \Vert \mathbf{A} + t \mathbf{B} \Vert_p\). If you set normalize to True, it plots the normalized function

\[\frac{\Vert \mathbf{A} + t \mathbf{B} \Vert_{p}}{ \Vert \mathbf{B} \Vert_p}.\]

To compare with the true values (without interpolation), pass compare=True to the above function.

Warning

By setting compare to True, every point in the array t is evaluated both using interpolation and with the exact method (no interpolation). If the size of t is large, this may take a very long run time.

>>> f.plot(t_array, normalize=True, compare=True)
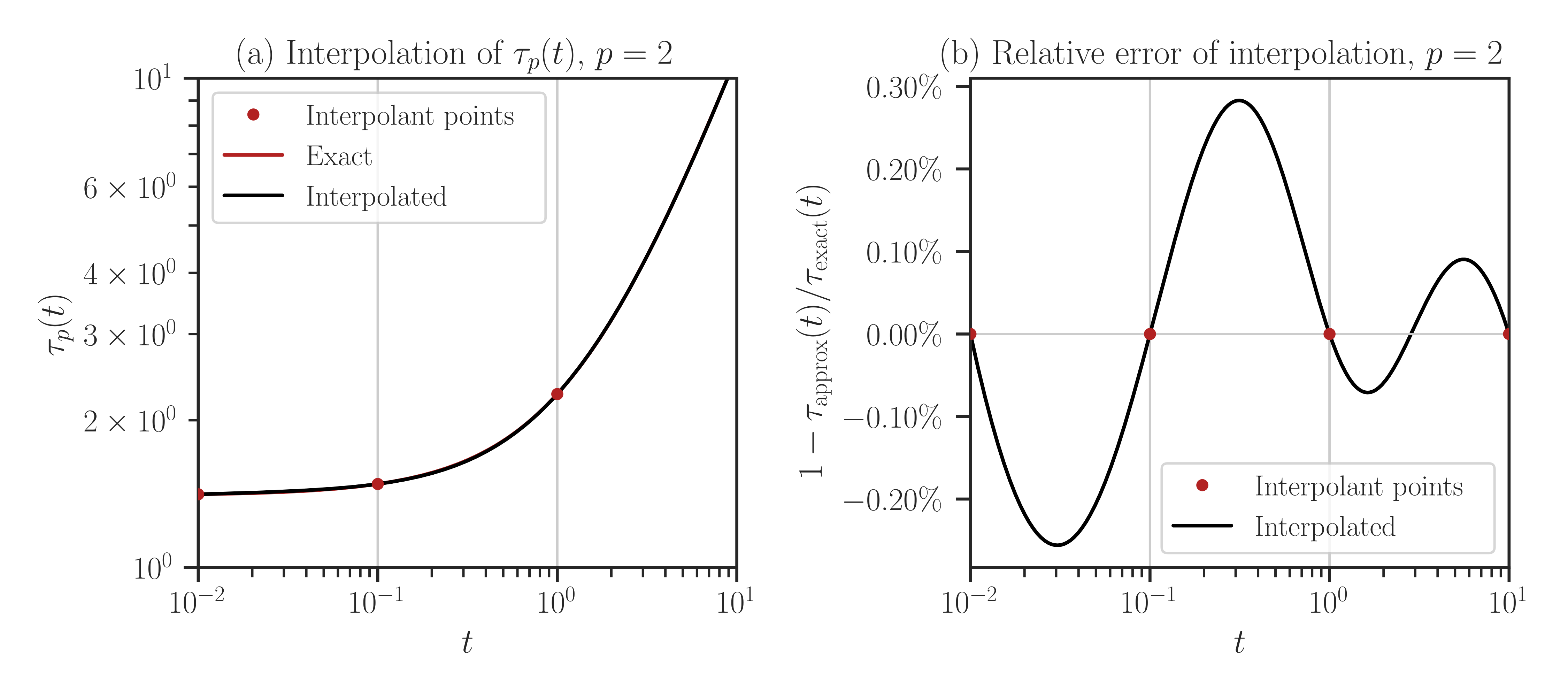
../_images/interpolate_schatten_3.png
Attributes:
kindstr

Method of interpolation

verbosebool

Verbosity of the computation process

nint

Size of the matrix

qint

Number of interpolant points

pfloat

Order of Schatten \(p\)-norm

Methods

__call__(t)

Interpolate at the input point t.

eval(t)

Evaluate the exact value of the function at the input point t without interpolation.

interpolate(t)

Interpolate at the input point t.

get_scale()

Returns the scale parameter of the interpolator.

bound(t)

Bound of the interpolation function.

upper_bound(t)

Upper bound of the interpolation function.

plot(t[, normalize, compare])

Plot the interpolation results.