imate.InterpolateLogdet.lower_bound

InterpolateLogdet.lower_bound(t)

Bound of the interpolation function.

If \(p < 1\), this function is a lower bound, and if \(p > 1\), this function is an upper bound of the interpolation function.

Parameters:

tfloat or numpy.array

An inquiry point or an array of inquiry points.

Returns:

boundfloat or numpy.array

Bound function evaluated at t. If t is an array, the output is also an array of the size of t.

See also

imate.InterpolateSchatten.bound

Notes

A lower bound for \(\mathrm{logdet}(\mathbf{A} + t \mathbf{B})\) is obtained as follows. Define

\[\Vert \mathbf{A} \Vert_0 = \left| \mathrm{det}(\mathbf{A}) \right|^{\frac{1}{n}}\]

Also, let

\[\tau_0(t) = \frac{ \Vert \mathbf{A} + t \mathbf{B} \Vert_0} {\Vert \mathbf{B} \Vert_0}\]

and \(\tau_{0, 0} = \tau_0(0)\). A sharp bound of the function \(\tau_0(y)\) is (see [1], Section 3):

\[\tau_{0}(t) \geq \tau_{0, 0} + t, \quad t \in [0, \infty).\]

The above inequality originate from the Brunn-Minkowski determinant inequality.

References

[1]

Ameli, S., and Shadden. S. C. (2022). Interpolating Log-Determinant and Trace of the Powers of Matrix \(\mathbf{A} + t \mathbf{B}\). Statistics and Computing 32, 108. https://doi.org/10.1007/s11222-022-10173-4.

Examples

Create an interpolator object \(f\) using four interpolant points \(t_i\):

>>> # Generate sample matrices (symmetric positive-definite)
>>> from imate.sample_matrices import correlation_matrix
>>> A = correlation_matrix(size=20, scale=1e-1)
>>> B = correlation_matrix(size=20, scale=2e-2)

>>> # Initialize interpolator object
>>> from imate import InterpolateLogdet
>>> ti = [1e-2, 1e-1, 1, 1e1]
>>> f = InterpolateLogdet(A, B, ti=ti)

Create an array t and evaluate upper bound on t. Also, interpolate the function \(f\) on the array t.

>>> # Interpolate at an array of points
>>> import numpy
>>> t = numpy.logspace(-2, 1, 1000)
>>> lb = f.lower_bound(t)
>>> interp = f.interpolate(t)

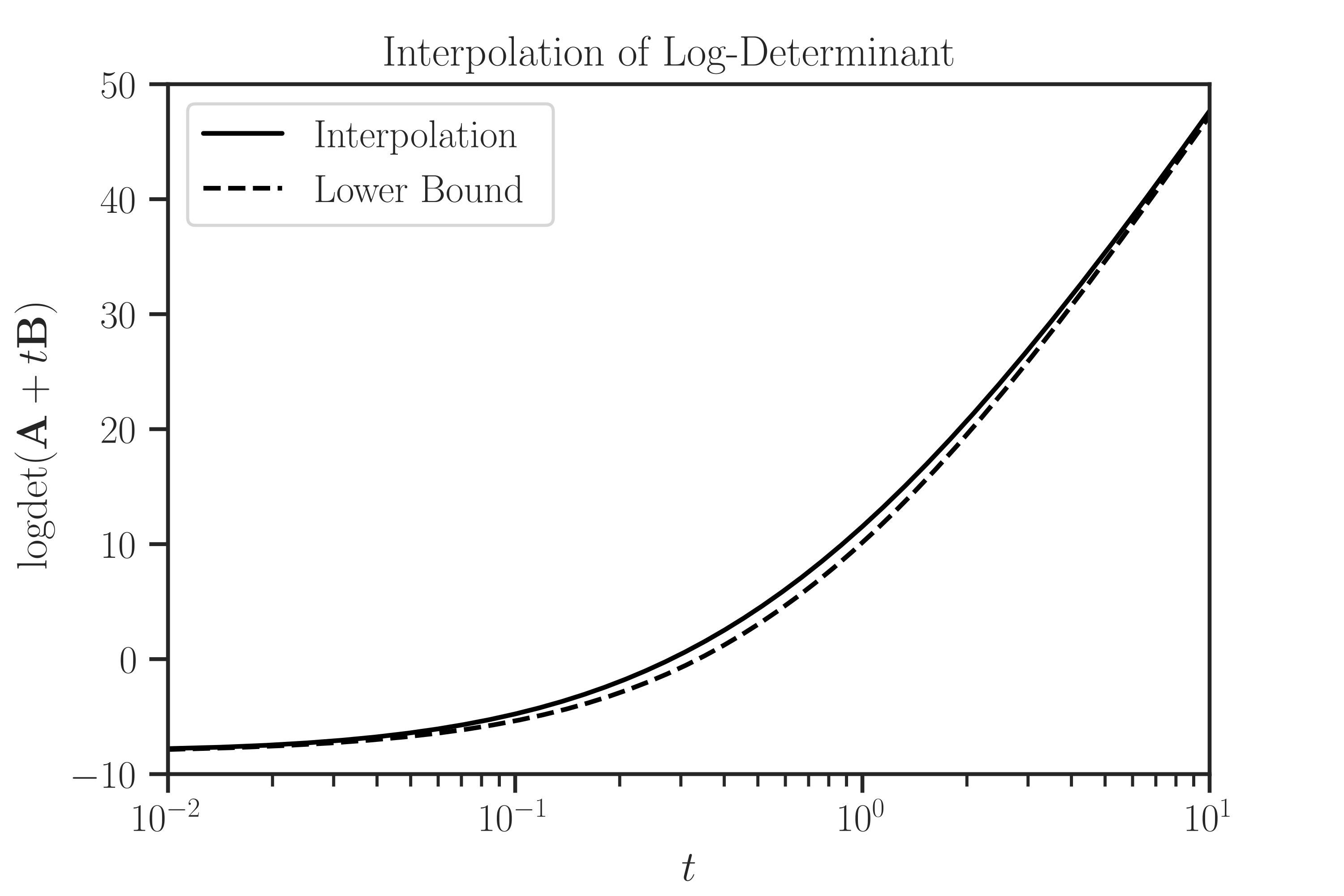
Plot the results:

>>> import matplotlib.pyplot as plt

>>> # Plot settings (optional)
>>> from imate._utilities import set_custom_theme
>>> set_custom_theme(font_scale=1.15)

>>> plt.semilogx(t, interp, color='black', label='Interpolation')
>>> plt.semilogx(t, lb, '--', color='black', label='Lower Bound')
>>> plt.xlim([t[0], t[-1]])
>>> plt.ylim([-10, 50])
>>> plt.xlabel('$t$')
>>> plt.ylabel('$\mathrm{logdet}(\mathbf{A} + t \mathbf{B})$')
>>> plt.title('Interpolation of Log-Determinant')
>>> plt.legend()
>>> plt.show()